После того, как автор сайта смог научить своего бота решать Линейное диофантово уравнение онлайн, возникло желание научить бота решать подобные уравнения, но уже с тремя неизвестными. Пришлось окунутся в книги.
Вынырнув оттуда через два месяца, автор понял, что он ничего не понял. Зело умные математики, так мудрёно писали алгоритм вывода формул, что мне смертному было стыдно. Опечалился было, но мысль на книжных просторах все таки одну полезную нашел, и с этой мысли пришло понимание как решать диофантовые уравнения с тремя неизвестными.
Итак для всех, кто не математик, но хочет им быть :)
Обновление от 11 декабря 2019 года: Решение системы из двух однородных диофантовых уравнений
Обновление от 17 сентября 2019 года: Есть калькулятор который высчитывает частное решение линейного диофантового уравнения с любым количеством неизвестных. Просьба оценить и если есть замечания написать.
Обновление октябрь 2020 года: Общее решение в виде матрицы. Прошу обратить внимание
Диофантовое уравнение с тремя неизвестными имеет вот такой вид
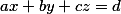
где 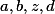 целые числа
целые числа
Если мы подумаем какое же общее решение может быть у неизвестных, то самое банальное выглядит так
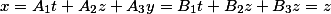
Подставим наше общее решение в уравнение
получим +b(B_1t+B_2z+B_3)+cz=d)
Какой же от этого прок, спросит нетерпеливый читатель? А вот какой, сгруппируем все по неизвестным,получим
+z(aA_2+bB_2+c)+A_3+B_3=d)
Смотрите, в правой части стоит какое то постоянное число, обозначенное буквой d
Значит, от t ( она же переменная, мало ли каким она значением хочет стать) оно не зависит а значит =0)
Логично предположить что и от z оно не зависит а значит =0)
а вот от постоянных значений A3 и B3 оно зависит напрямую , то есть 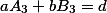
Что же в конечном итоге мы получили? А получили мы три типовых классических диофантовых уравнений с двумя неизвестными, которые решать мы можем легко и непринужденно.
Попробуем решить?
В первых строках поисковых систем нашлось вот такое уравнение 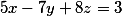
Первое уравнение будет вот такое
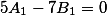
корни его
k Y= 0 - (5)k)
Избавимся от нулей, взяв к примеру k=-1. ( Хотите можете взять 2 или 100 или -3) На окончательное решение это не повлияет.
тогда 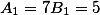
Решаем второе уравнение
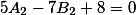
и его корни
k Y= -6 - (5)k)
здесь пусть k=0 ( так как X и Y не совпадают уже при нулевых значениях)
получим
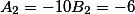
И последнее третье уравнение
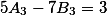
Корни тут такие
kY= 1 - (5)k)
то есть 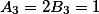
Подставим теперь все найденные значения в общий вид
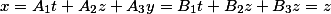
получим
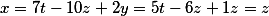
Вот и все!
Заметьте, что все решается очень легко и прозрачно! Наверняка преподаватели и способные студенты возьмут себе на вооружение эту методику, так как в книгах автор бота её так и нашел.
Еще один пример, уже решенный с помощью бота.
| Результат решения диофантового уравнения с тремя неизвестными |
y+(22)z=11) |
| Целочисленные корни такого уравнения следующие |
t+(2)) |
t+(-1)) |
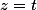 |
Дополнение: Когда будете решать подобные уравнения с помощью бота, можете столкнуться с тем, что бот Вам выдаст ошибку с просьбой, поменять переменные местами, для другой попытки решить уравнение. Это связано с тем что при промежуточных вычислениях, получается нерешаемое уравнение
Как пример
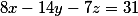
При попытке решить уравнение
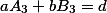
в нашем случае 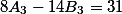
мы получим ошибку, так как при любых значениях, в левой части будет всегда(!!) чётное число, а в правой части как мы видим нечетное.
Но это не значит что изначальное уравнение нерешаемое. Достаточно поменять слагаемые в другом порядке, например так
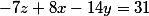
и получаем ответ
| Целочисленные корни такого уравнения следующие |
t+(7)) |
t+(10)) |
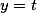 |
Дополнение от 23 ноября 2015 года
Зашел спор как решать уравнение подобное этому
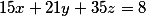
Мол, позволяет ли методика которая была описана выше определить существует ли целочисленные решения этому уравнению?
Я не могу доказать, но предполагаю, что если при всех циклических перестановках слагаемых как это было показано на примере уравнения 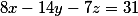 у нас получаются нерешаемые линейные уравнения, то такое уравнение нерешаемое.
у нас получаются нерешаемые линейные уравнения, то такое уравнение нерешаемое.
В нашем примере так и получается что при любых переставновках, в левой части линейного уравнения всегда(!) будут НЕ взаимно простые числа, и НОД их не является делителем числа в правой части уравнения ( =8 )
Таким образом утверждается что такое диофантовое уравнение нерешаемое в целых числах, но зато оно решается в случае рациональных дробей
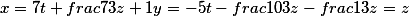
при любых значениях z и t уравнение будет верным
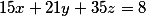
По горячим следам, окончательное дополнение от 23 нобяря 2015
Все таки я ошибся в последнем примере... решаемое оно
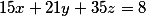
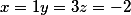
Так что вышеописанная методика и бот, применим ТОЛЬКО для тех случаев, когда хотя бы одна пара слагаемых из левой части являются взаимно простыми числами.
Если конечно не воспользуетесь новым калькулятором который лишен, всех этих недостатков
Частное решение диофантового уравнения с несколькими неизвестными
Удачных расчетов!!