Представим себе задачу, есть круг радиусом и есть две перпендикулярные прямые, точка пересечения которых находится внутри круга.
Они делят круг на четыре части. Вопрос: чему равны их площади ?
Упростим вопрос и попробуем узнать чему равна площадь закрашенной фигуры?
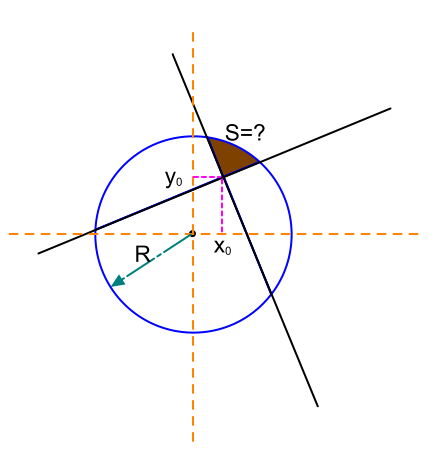
При должной смекалке и недолгих раздумий, данную задачу можно решить любому, кто знает как вычислять сегмент и площадь круга.
"Покрутим" изображение таким образом, что бы перпендикулярные линии были параллельны осям ординат и абсцисс. Площадь, которую мы хотим найти, от этого поворота никак не изменилась.
Именно это мы и будем считать исходными данными.
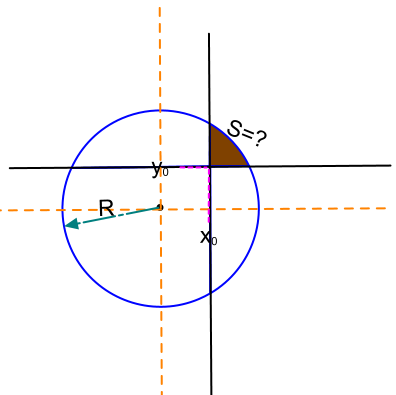
Начнем считать?
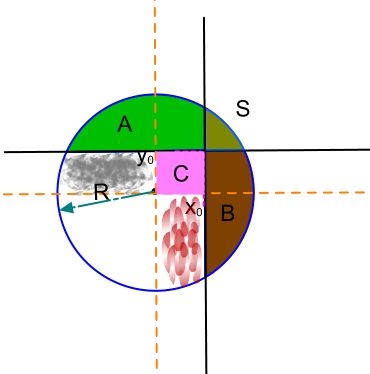
\(A\) - это у нас первый круговой сегмент, площадь которого мы можем найти.
\(B\) - это второй круговой сегмент, который тоже легко высчитывается
\(S\) - этот "кусочек" входит и в сегмент \(A\) и в сегмент \(B\), поэтому закрашен коричнево-зеленой краской.
Площадь розового прямоугольника \(C\) высчитывается как произведение \(x_0*y_0\)
Область, закрашенная серым, в левой части круга, высчитывается как разница площади четверти круга и половине сегмента \(A\)
А область, отмеченная красными мазками, высчитывается как разница площади четверти круга и половине сегмента \(B\)
И осталась белая, незакрашенная область, равная четверти площади круга.
Просуммируем?
\(A+B-S+C+\cfrac{R^2\pi}{4}-\cfrac{A}{2}+\cfrac{R^2\pi}{4}-\cfrac{B}{2}+\cfrac{R^2\pi}{4}=R^2\pi\)
Сгруппируем, перенесем и получим
\(S=C+\cfrac{A}{2}+\cfrac{B}{2}-\cfrac{R^2\pi}{4}\)
Теперь вспоминаем формулы площади кругового сегмента и прямоугольника.
\(С=x_0*y_0\)
\(A=\cfrac{R^2}{2}(2acos(\cfrac{y_0}{R})-sin(2acos(\cfrac{y_0}{R})))\)
\(B=\cfrac{R^2}{2}(2acos(\cfrac{x_0}{R})-sin(2acos(\cfrac{x_0}{R})))\)
В принципе на этом можно и остановится, но мы углубимся в своих изысканиях
Подставим все в конечную формулу и получим вот такого "монстрика"
\(x_0*y_0+\cfrac{R^2}{2}acos(\cfrac{1}{R^2}(x_0*y_0-\sqrt{(R^2-x_0^2)(R^2-y_0^2)}))-\cfrac{x_0}{2}\sqrt{R^2-x_0^2}-\cfrac{y_0}{2}\sqrt{R^2-y_0^2}=S\)
Удачных расчетов!