| Общее решение произвольного диофантового уравнения |
![Исходные данные]() |
| Созданное по матрице диофантовое уравнение |
![Решение системы]() |
Продолжим развивать тему диофантовых уравнений и рассмотрим следующую задачу: Пусть мы знаем какую либо общую систему решения какого либо линейного однородного диофантового уравнения с несколькими переменными.
В нашем случае это выглядит так
Исходное уравнение
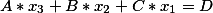
Общее решение
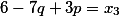
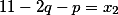
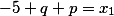
Следует по общему решению найти коэффициенты первоначального уравнения.
Первое, что приходит в голову это подставить в исходное выражение общее , группировать, сокращать подобное и наверное получить правильный результат.
Почему "наверное"?
Потому что такая мысль мне в голову и не приходила. Хотите проверяйте, это не моё.
Другая идея может состоять в том что бы из общей системы вычислив несколько значений, решить систему линейных уравнений . Такая идея не лишена смысла, но опять это не мой метод.
Я пошел как всегда иным путем и воспользовавшись созданным калькулятором ФРС. Фундаментальное решение системы уравнений, решил эту и подобные задачи.
Введя коэффициенты общего решения
\(\begin{pmatrix}6&-7&3\\11&-2&-1\\-5&1&1\end{pmatrix}\)
мы получим чудесный и самое главное правильный ответ
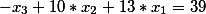
Еще один пример
Общая система уравнений
\(-9x_{1}+3x_{2}+2x_{3}+1=0\\ 1x_{1}+11x_{2}+9x_{3}+8=0\\ 13x_{1}+8x_{2}+5x_{3}-7=0\\ 1x_{1}+0x_{2}-1x_{2}+1=0\)
Диофантовое уравнение созданное по матрице
\((129)*y_{4}+(-72)*y_{3}+(78)*y_{2}+(219)*y_{1}=-774\)