Рассмотрим интересную задачу по делению произвольного треугольника N параллельными линиями ( относительно какой либо стороны) на части , площадь которых одинакова. Данную задачу никто не изучал, поэтому возьмемся за неё.
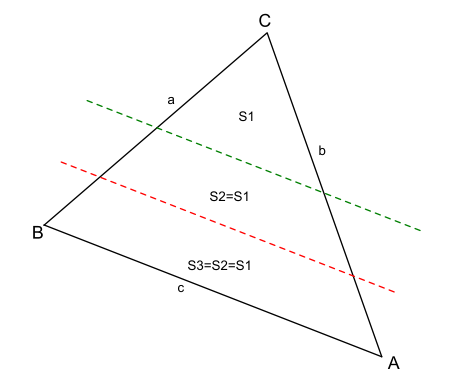
Нам надо определить на каком расстоянии от стороны \(c\) , провести красную линию и зеленую линию, параллельную стороне \(c\), так что бы площади \(S_1=S_2=S_3\) были равны.
Исходя из принципа, уже примененного в материалах Деление шара на равные объемы параллельными плоскостями мы можем заметить, что несмотря на сколько частей мы будем делить наш треугольник, всегда будет у нас трапеция с основанием \(c\)
Общая площадь треугольника \(ABC\) можно выразить так \(S=\cfrac{c*h}{2}\), где \(h\) - высота треугольника
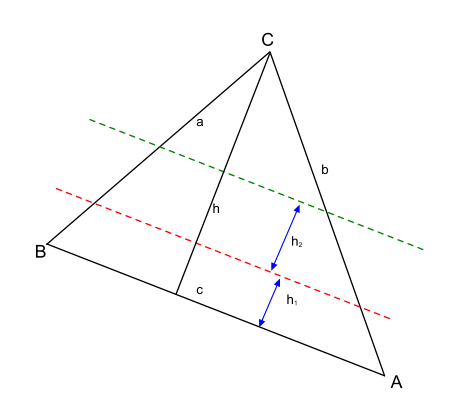
Площадь трапеции ограниченной красной линией и основанием равна произведению их полу суммы и высоты \(h_1\)
\(S_t=\cfrac{h_1(redline+c)}{2}\)
Разделив общую площадь треугольника на \(n\) равных частей мы можем написать равенство.
\(\cfrac{c*h}{2n}=\cfrac{h_1(redline+c)}{2}\)
или после преобразований
\(\cfrac{1}{n}=\cfrac{h_1}{h}(2-\cfrac{h_1}{c}(\cfrac{1}{tan(A)}+\cfrac{1}{tan(B)}))\)
И вроде бы все хорошо, получается квадратное уравнение, где мы можем найти \(h_1\), но количество исходных данных превышает все разумные границы.
Как же нам узнать и избавится от вычислений углов \(A\) и \(B\)
Сделаем красивое, а значит и простое предположение.
Пусть этот же исходный треугольник мы разделим на 1 часть ( ну то есть фактически оставив его целым)
Тогда высота \(h_1=h\) и следовательно уравнение будет иметь вид
\(\cfrac{1}{1}=\cfrac{h}{h}(2-\cfrac{h}{c}(\cfrac{1}{tan(A)}+\cfrac{1}{tan(B)}))\)
или \(\cfrac{1}{tan(A)}+\cfrac{1}{tan(B)}=\cfrac{c}{h}\)
Формула очень элегантна и красива, если же мы её попытаемся преобразовать, то придем, к "страшненькой" но очень известной по всем справочникам формуле
\(h=c\cfrac{sin(A)sin(B)}{sin(A+B)}\)
Почему "страшненькая"? Потому что зная например основание, высоту и один из углов, второй угол вычислить без "кувырканий" совершенно невозможно. в отличии от формулы
\(\cfrac{1}{tan(A)}+\cfrac{1}{tan(B)}=\cfrac{c}{h}\)
Но мы отвлеклись от основной темы...
Подставим нашу формулу в первоначальную и получим, после сокращений, вот такое квадратное уравнение:
\(\cfrac{h_1^2}{h^2}-2\cfrac{h_1}{h}+\cfrac{1}{n}=0\)
Какие же выводы мы может сделать?
А то, что любой (любой!!) треугольник с разными сторонами или углами, но имеющих одинаковую высоту, делится всегда в одной пропорции
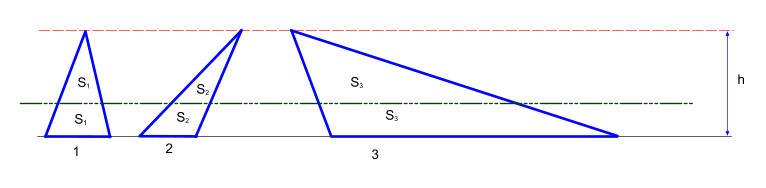
Взяв от высоты треугольника 0.2928932188135 часть и проведя параллельную линию основания треугольника - мы гарантировано разделим его на две равные части.
Как же мы можем проверить столь необычный вывод?
А мы можем вычислить длину секущей(параллельной прямой) в треугольнике, по методу, который гласит - в подобных треугольниках площади относятся как как квадраты линейных размеров.
То есть если основание какого либо треугольника равно например 10, то меньший подобный треугольник, который получается отсечением по красной линии ( см исходный рисунок) имеет основание \(redline=\cfrac{10}{\sqrt(2)}=7.071\)
теперь можно узнать площадь трапеции \(\cfrac{10+7.0.71}{2}*0.2928932\) и эта площадь есть половина от площади всего треугольника с основанием 10 и высотой 1., то есть равна 2.5
Фактически последний метод позволяет и без формул узнавать новые высоты треугольника( так как она имеет тоже линейные размеры), но все равно считаю что статья написана не зря.
Что бы разделить треугольник на три части, то высота первой трапеции равна \(1-\sqrt{\cfrac{2}{3}}\), что бы разделить на десять частей, первая высота от основания равна \(1-\sqrt{\cfrac{9}{10}}\), ну и так далее.