| Каноническое уравнение гиперболы |
![Введенное выражение]() |
| Большая полуось гиперболы |
|
| Малая/мнимая полуось гиперболы |
|
| Эксцентриситет гиперболы |
|
| Фокальный параметр |
|
| Фокальное расстояние |
|
| Перицентрическое расстояние |
|
Уравнение гиперболы в каноническом виде имеет вот такой вид.
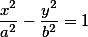
Так же как и при расчете уравнения эллипса по двум точкам, мы можем по двум точкам однозначно построить гиперболу, выраженную через вышеуказанную формулу.
Используя универсальный калькулятор расчет кривой второго порядка на плоскости по точкам, мы легко определим значения  и
и 
Кроме этого, зная эти параметры можно рассчитать следующее:
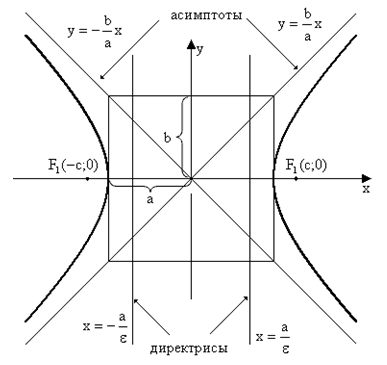
Большая полуось  - расстояние от центра гиперболы, до одной из вершин
- расстояние от центра гиперболы, до одной из вершин
Фокальное расстояние  - расстояние от центра гиперболы до одного из фокусов
- расстояние от центра гиперболы до одного из фокусов
Мнимая полуось  - расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат
- расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат
Связь между тремя параметрами выражена в одной формуле
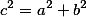
Эксцентриситет - коэффициент, численно равный, отношению фокусного расстояния к большой полуоси гиперболы
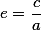
Фокальный параметр -расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат
Прицельный параметр - расстояние от фокуса до асимптоты. Численно равен малой полуоси гиперболы.
Перицентрическое расстояние -расстояние от фокуса до ближайшей вершины гиперболы
)
Примеры задач
Cоставить каноническое уравнение гиперболы по двум точкам ;M_2(-2\sqrt{5}:3))
Вводим данные в поля ввода. Можем писать как выражение, учитвая что квадратный корень обозначается sqrt, а можем сначала получить численные значения и подставить уже окончательные результаты.
В результате получим
|
Каноническое уравнение гиперболы |
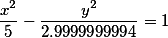 |
|
Большая полуось гиперболы |
|
4.47213595499958
|
|
Малая/мнимая полуось гиперболы |
|
3.4641016147913444
|
|
Эксцентриситет гиперболы |
|
1.1661903789073205
|
|
Фокальный параметр |
|
1.79999999928
|
|
Фокальное расстояние |
|
5.830951894536603
|
|
Перицентрическое расстояние |
|
0.8309518945366023
|
Есть небольшая погрешность в вычислениях, вместо 2.9999999999 должно быть 3. Но думаю, что клиенты отнесутся с снисхождением, к одной десяти миллионной погрешности.
Удачных расчетов!