Гипербола первого порядка. Нелинейная регрессия

Значения аргументов X, через пробел

Значения функции Y=f(X), через пробел

Исходные данные Xi=Yi

По заданным параметрам рассчитана эмпирическое уравнение регрессии

Регрессионная формула

Продолжаем наши расчеты нелиненых регрессий. Кроме эмпирических формул, выражающихся через формулу параболы второго или третьего порядка существуют еще формула корреляционной связи через гиперболу.

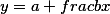
$y=a+/frac{b}{x}$

где a,b- неизвестные коэффициенты которые и надо найти, при известных измерениях Y и X

Для этого мы должны будем решить систему линейных уравнений

http://abak.pozitiv-r.ru

$sum{y}=an+bsum{frac{1}{x}}sum{frac{y}{x}}=asum{frac{1}{x}}+bsum{frac{1}{x^2}}$

можно решать матричным способом, но есть уже рассчитанные формулы, которыми мы и воспользуемся

$a=frac{1}{D}(sum{y}sum{frac{1}{x^2}}-sum{frac{y}{x}}sum{frac{1}{x}}$

$b=frac{1}{D_2}(sum{(x-x_s)y{sum{(x-x_s)^2)$

где определитель системы

$D=(nsum{frac{1}{(x-x_s)^4}}-(sum{frac{1}{(x-x_s)^2}})^2$

n - число членов ряда регресии

y - значения переменной Y

x - значения переменной X

Если вы будете пользоваться этим ботом через XMPP клиента, то синаксис такой

regress ряд X;ряд Y;3

где 3 - показывает что регрессию считаем, как гиперболу первого порядка

Что ж, пора проверить наши расчеты.

Итак есть таблица

X	Y
1.4	673
2.2	489
2.3	451
2.6	405
3.6	485
4.1	330
4.4	288
5.8	268

надо определить коэффиценты a, b

Не смотря на то, что есть функция regress для пользователей XMPP клиентов , нам удобнее вводить данные через WEB интерфейс.

Удачных расчетов!

Поиск по сайту

Главная |---| Экономика и финансы |---| Гипербола первого порядка. Нелинейная регрессия