В этом материале мы рассмотрим решение уравнения вида
\(cos(2x+P)=b*cos(x+Q)\)
Такое уравнение имеет 4 различных корня(в одном периоде).
В отличии от других калькуляторов, мы такое уравнение будем рассчитывать не приближенными методами, как это делается в большинстве случаев, а через полином 4 степени.
В одной из предыдущих статьей, мы решали полное уравнение четвертой степени по своей методике, и теперь мы можем с полным правом использовать свои наработки.
Как и всегда коэффиценты в данном уравнении могут быть и вещественными и мнимыми, или состоять из математического выражения.
А теперь инструкция, как из исходного уравнения получить многочлен 4 степени.
\(cos(2x+P)=b*cos(x+Q)\)
Представляем косинус как
\(cos(x)=\cfrac{e^{ix}+e^{-ix}}{2}\)
Тогда
\(\cfrac{e^{i2x+pi}+e^{-2ix-pi}}{2}=b\cfrac{e^{ix+qi}+e^{-xi-qi}}{2}\)
Преобразуем его
\({e^{i2x}*e^{pi}+e^{-2ix}*e^{-pi}}=b({e^{iq}*e^{xi}+e^{-qi}*e^{-xi}})\)
Если представить \(e^{ix}=y\) то получим
\(y^2*e^{pi}+\cfrac{e^{-pi}}{y^2}=b(e^{-qi}*\cfrac{1}{y}+e^{qi}*y)\)
избавимся от знаменателя
\(y^4*e^{pi}+{e^{-pi}}=b(e^{-iq}*{y}+e^{qi}*y^3)\)
И вот оно уравнение 4 степени. Можем еще чуть преобразовать и получим окончательно
\(y^4+{e^{-2pi}}=b(e^{-iq-pi}*{y}+e^{qi-pi}*y^3)\)
\(y^4-be^{qi-pi}*y^3-be^{-iq-pi}*{y}+{e^{-2pi}}=0\)
Никто в здравом уме и не соберется вручную решать это по методу Феррари или любым другим способом. Но у нас есть калькулятор, который спокойно выдаст все 4 решения.
несколько примеров
\(cos(2x+5)=11*cos(x+1)\)
\(y^4-11e^{-4i}*y^3-11e^{-6i}*{y}+{e^{-10i}}=0\)
Ввводим коэффициенты 1 -11*e^(-4i) 0 -11*e^(-6i) e^(-10i)
Найти корни уравнения, многочлена 4 степени онлайн
| Исходный многочлен |
)*x^3+(0)*x^2+(-11*e^(-6i))*x^1+(e^(-10i))) |
| Кубическая резольвента |
*x^2+(-10908.50481417+3415.9962243617i)*x^1+(-114084.61778484-223045.72471649i)) |
| Корни кубической резольвенты |
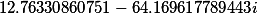 |
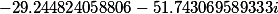 |
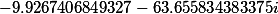 |
| Корни заданного многочлена 4 степени |
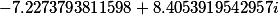 |
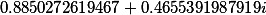 |
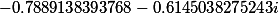 |
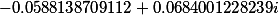 |
| Вспомогательные коэффициенты |
F2=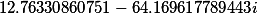 |
F1=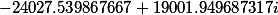 |
T=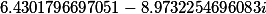 |
теперь взяв логарифм каждого корня, разделенный на мнимую единицу мы получаем
2.280981314-2.405627029i
0.484243759-0i
-2.479835772-0i
2.280981314+2.405627029i
значения которые являются корнями уравнения
\(cos(2x+5)=11*cos(x+1)\)
Удачных расчетов!