| Заданная функция |
![Введенное выражение]() |
|
Рассмотрим одну из простых и незаслужено забытых на просторах интернета методики определения производной полинома, произвольной (положительной) степени.
До последнего был уверен, что если известен многочлен вида
=a_0x^{n}+a_1x^{n-1}+a_2x^{n-2}+.....+a_{n-1}x+a_n)
и необходимо узнать значение производной например 5 порядка в какой либо точке, необходимо сначала вычислить эту производную (пятого порядка), а потом уже подставив значение, рассчитать производную.
Оказывается есть более простой и алгоритмически легкий способ, нахождения производной в точке.
Для этого нам понадобится методика описанная в материалах: Разложить многочлен по степеням и Метод Горнера. Деление многочлена.
Да, да, оказывается метод Горнера с успехом решает поставленную задачу.
Рассмотрим пример:
Вычислить производную третьего порядка при х=3 следующего многочлена
=2x^3-5x^2+x+7)
1. Разделим заданный многочлен на 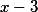
Получим =2x^2+x+4) и остаток 19.
и остаток 19.
Число 19 есть значение функции =2x^3-5x^2+x+7) если мы подставим туда x=3
если мы подставим туда x=3
2. Разделим =2x^2+x+4) снова на
снова на 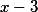
Получим =2x+7) и остаток 25.
и остаток 25.
Так как это первая проивзодная, то умножим полученный результат на 1!(один факториал)=1. Получили то же число 25
Число 25 это значение первой производной от заданной функции при x=3. То есть если мы вычислим первую производную
=6x^2-10x+1) и подставим туда значение 3 получим тот же ответ = 25.
и подставим туда значение 3 получим тот же ответ = 25.
3. Разделим =2x+7) снова на
снова на 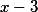
получим =2) и остаток 13.
и остаток 13.
Умножим это число на 2! (два факториал) =2 и мы получим значение производной функции второго порядка при х=3
Это число =26
4. Производная третьего порядка вычисляется в данном случае просто, так как =2) далее уже делить невозможно, то это и является остатком. Его необходимо умножить на 3!(три факториал)=6
далее уже делить невозможно, то это и является остатком. Его необходимо умножить на 3!(три факториал)=6
И получим, что производная третьего порядка при заданном многочлене при x=3 равна 12.
Таким незамысловатым способом мы можем находить значения любой производной любого полинома.
Алгоритм прост, но при многочленах со степенями выше 10, мы сталкиваемся с необходимостью вычислять факториалы выше 10, что очень трудоемко, так как факториал от 10 равен 3628800, а факториал от 16 уже 20922789888000
Но нам на пользу приходит одно из свойств методики Горнера, которое гласит: Если мы умножим какую либо функцию на число то и остаток отделения возрастет во столько же раз.
Поэтому нам достаточно умножать полученные коэффиценты полинома от деления на числа 1,2,3,4,5 и т.д. в зависимости от того какую производную мы вычислем в данный момент и вычислить остаток.
Калькулятор работает и в поле комплексных чисел, поэтому решим вот такой пример.
Есть функция =2x^7+(1-5i)x^6 -7x^4+x^3i+2x^2 -9x-1)
Необходимо узнать все возможные производные этой функции при x=i
Несложно убедится что решая это вручную, можно допустить оплошность и пойти по неверному пути.
Намного проще воспользоватся ботом и через XMPP клиент написать
propol 2 1-5i 0 -7 i 2 -9 -1;i
и мы получим все результаты
Найдены значения производной полинома
0 производная. Значение функции -10-6i
1 производная. Значение функции 7+35i
2 производная. Значение функции 112-66i
3 производная. Значение функции -180-282i
4 производная. Значение функции -528+120i
5 производная. Значение функции -1440+720i
6 производная. Значение функции 720+6480i
7 производная. Значение функции 10080
Логичный вопрос - а что же такое нулевая производная?
Ответим - это исходная функция. А значение -10-6i получается если бы мы -i подставили в исходную функцию
Попробуем решить другое уравнение
знаем чему же равна четвертая производная функции
=(7-i)x^{17}+2x^{11} -ix^7+9x-5)
при х=2+i
Полином 17-ой степени.. это серъезно как и вычисление при комплексном аргументе.
Что ж попробуем
|
Заданная функция |
=(7-i)*x^{17}+(2)*x^{11}+(-i)*x^{7}+(9)*x^{1}+(-5)*x^{0}) |
|
Производная |
Значение производной при X=2+i |
|
0 |
707043+6123674i |
|
1 |
25630678+39273242i |
|
2 |
289802562+169486216i |
|
3 |
2247959580+147950190i |
|
4 |
13006113720-5465417040i |
|
5 |
53432793120-62240220840i |
|
6 |
107126132400-427018989600i |
|
7 |
-468058852800-2114656795440i |
|
8 |
-6101588908800-7522728998400i |
|
9 |
-35506871769600-16099283692800i |
|
10 |
-1.393813225728E+14+5293047513600i |
|
11 |
-3.828579156864E+14+2.0995438464E+14i |
|
12 |
-6.6691392768E+14+9.6332011776E+14i |
|
13 |
-3.705077376E+14+6.1024803840002E+14i |
|
14 |
1.4820309504E+15+7.8460462080004E+14i |
|
15 |
5.2306974720004E+14+5.230697472E+14i |
|
16 |
3.1384184832005E+14+1.0461394944E+14i |
|
17 |
24.89811996672http://abak.pozitiv-r.ru |
|
при значении x=2+i значение функции при взятии четвертой производной будет
|
4 |
13006113720-5465417040i |
Что еще можно заметить?
Что необходимо внимательно смотреть на расчеты.
В нашем примере при взятии 17 призводной получается число 24.898
хотя должно конечно же быть
(17!))
где 17! это факториал от
17 = 355687428096000
Это небольшая недоработка (ошибка при вычислении больших производных) будет испарвлена в ближайшее время. Но вычисления производных не выше 10 порядка, бот осуществляет правильно.
Удачных расчетов!