| Вы ввели следующие элементы массива |
|
| Обратная квадратная матрица |
|
| В виде строки |
|
Матрица называется обратной для квадратной матрицы A если \(AA^{-1}=A^{-1}A=E\)
где E - единичная матрица ( т.е матрица на главной диагонали которой стоят единицы, а все остальные элементы равны нулю)
\(e=\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}\)
Квадратная матрица А называется вырожденной, если её определитель равен нулю, и невырожденной в противном случае.
Если матрица А имеет обратную, то эта матрица невырожденная.
Верно и обратное утверждение. Всякая невырожденная матрица.
\(a=\begin{pmatrix}a_{11}&a_{12}&...&a_{1n}\\a_{21}&a_{22}&...&a_{2n}\\...&...&...&...\\a_{n1}&a_{n2}&...&a_{nn}\end{pmatrix}\)
имеет обратную матрицу
\(a^{-1}=\frac{1}{det(a)}\begin{pmatrix}a_{11}&a_{12}&...&a_{1n}\\a_{21}&a_{22}&...&a_{2n}\\...&...&...&...\\a_{n1}&a_{n2}&...&a_{nn}\end{pmatrix}\)
Где Aij - алгебраическое дополнение матрицы
Например исходная матрица
\(\begin{pmatrix}1&3&-5&11\\1+i&0&-3&1.66\\0.6&7&1&-7\\-2&-2-4i&0&10\end{pmatrix}\)
А это обратная, с округлением до 4 знаков после запятой
\(\begin{pmatrix}0.3232+0.3544i&-0.4955-0.7294i&0.1294-0.4163i&-0.1827-0.5601i\\0.0327+0.018i&-0.0063-0.0194i&0.1445+0.0318i&0.0663+0.0057i\\0.025+0.2743i&-0.3066-0.4925i&0.2052-0.1062i&0.167-0.2943i\\0.064+0.0876i&-0.0926-0.1523i&0.0421-0.0191i&0.0745-0.0844i\\\end{pmatrix}\)
Какая практическая ценность обратной матрицы? Где мы можем ее использовать?
Самый простой пример и наглядный.
У нас есть система уравнений
\(5x_1+3x_2=h_1\\3x_1+2x_2=h_2\)
Нам требуется выразить 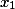 и
и 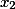 через
через 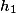 и
и 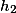
если мы возьмем от матрицы
\(\begin{pmatrix}5&3\\3&2\end{pmatrix}\) обратную, то получим \(\begin{pmatrix}2&-3\\-3&5\end{pmatrix}\)
И следовательно наше решение выглядит вот так
\(x_1=2h_1-3h_2\\x_2=-3h_1+5h_2\)
Еще несколько примеров
Исходная матрица \(\begin{pmatrix}1&3\\6&5\end{pmatrix}\)
Обратная матрица исходной, равна \(\begin{pmatrix}-0.3846&0.2308\\0.4615&-0.0769\\\end{pmatrix}\)
Матрица содержащаяя выражения
\(\begin{pmatrix}1 & 3 & -i\\ 6 & sin(2+i) & 5\\ ln(\frac{3}{(4-i)}) & i^{1.433} & -8\end{pmatrix}\)
после автоматического преобразования мы получаем вот такую матрицу
\(\begin{pmatrix}1 & 3 & 0-i \\ 6 & 1.4031-0.4891i & 5 \\ -0.318+0.245i & -0.6289+0.7775i & -8 \\ \end{pmatrix}\)
И обратная ей матрица имеет следующий вид
\(\begin{pmatrix}-0.0595+0.0033i & 0.1828-0.005i & 0.1147+0.0043i \\ 0.3425-0.009i & -0.0609+0.0009i & -0.0392-0.0423i \\ -0.0238+0.032i & -0.0024-0.0002i & -0.1225+0.0029i \\ \end{pmatrix}\)
Удачных расчетов!!