| Параметры пересечения двух прямых |
|
Перпендикулярная прямая
Это задача наверное одна из самых популярных и востребованных в школьных учебниках. Задачи, основанные на эту тему многообразны. Это и определение точки пересечения двух прямых, это и определение уравнения прямой, проходящяя через точку на исходной прямой под каким либо углом.
Эту тему мы раскроем, используя в своих вычислениях данные полученные с помощью Расчет параметров прямой линии по заданным параметрам
Именно там было рассмотрено преобразование общего уравнения прямой, в уравнение с угловым коэффициентом и обратно, и определения остальных парметров прямой по заданным условиям.
Что же нам не хвататет для того, что бы решать те задачи, которым посвящена эта страница?
1. Формулы вычисления одного из углов между двумя пересекающимися прямыми.
Если мы имеем две прямые которые заданы уравнениями:
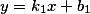и 
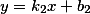
то один из углов вычисляется так:
=\frac{k_2-k_1}{1+k_2k_1})
2. Уравнение прямой с угловым коэффициентом, проходящяя через заданную точку )
)
Из формулы 1, мы можем увидеть два пограничных состояния
а) ког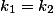да 
тогда =0)
и следовательно эти две заданные прямые паралельны ( или совпадают)
б) когда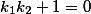 
, тогда =\infty)
, 
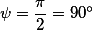и следовательно эти прямые перпендикулярны, то есть пересекаются под прямым углом.
Какие могут быть исходные данные для решения подобных задач, кроме заданной прямой?
- точка на прямой и угол под которым вторая прямая его пересекает
- второе уравнение прямой
Какие же задачи может позволить решить бот ?
1. Заданы две прямые ( явным или не явным образом например по двум точкам). Вычислить точку пересечения и углы по которыми они пересекаются.
2. Задана одна прямая , точка на прямой и один угол. Определить уравнение прямой, перескающую заданную под указанным углом
Примеры
Две прямые заданы уравнениями. Найти точку пересечения этих прямых и углы под которым они пересекаются
line_p A=11;B=-5;C=6,k=3/7;b=-5
получаем следующий результат
Уравнение первой прямой
y = 2.2 x + ( 1.2 )
Уравнение второй прямой
y = 0.4285714285714 x + ( -5 )
Угол пересечения двух прямых(в градусах)
-42.357454705937
Точка пересечения двух прямых
x = -3.5
y = -6.5
Не забудьте что параметры двух линий разделяются запятой, а параметры каждой линии точкой с запятой.
Прямая проходит через две точки (1:-4) и (5:2) . Найти уравнение прямой, которая проходит через точку (-2:-8) и пересекает исходную прямую под углом 30 градусов.
Одна прямая нам известна, так как известны две точки через которые она проходит.
Осталось определить уравнение второй прямой . Одна точка нам известна, а вместо второй указан угол, под которым первая прямая пересекает вторую.
Вроде все известно, но тут главное не ошибится. Речь идет об угле(30 градусов) не между осью абсцисс и линией, а между первой и второй линией.
Для этого мы постим так. Определим параметры первой линии, и узнаем под каким углом она пересекает ось абсцисс.
Для этого воспользуемся Расчет параметров прямой линии по заданным параметрам
line xa=1;xb=5;ya=-4;yb=2
Параметры прямой линии по заданным параметрам
Общее уравнение Ax+By+C = 0
Коэффициент А = -6
Коэффициент B = 4
Коэффициент C = 22
Уравнение прямой в отрезках x/a+y/b = 1
Коэффициент a= 3.6666666666667
Коэффициент b = -5.5
Уравнение прямой c угловым коэфициентом y = kx + b
Коэффициент k = 1.5
Угол наклона к оси ( в градусах) f = 56.309932474019
Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0
Коэффициент p = 3.0508510792386
Коэффициент q = 2.5535900500422
Расстояние между точками=7.211102550928
Расстояние от точки до прямой li =
Видим что первая линия пересекает ось под углом 56.309932474019 градусов.
В искходных данных не сказано как именно пересекает вторая линия, первую. Можно ведь построить две линии удовлетворяющих условиям, первая повернутая на 30 градусов ПО часовой стрелке, а вторая на 30 градусов ПРОТИВ часовой стрелке.
Давайте их и посчитаем
Если вторая линия повернута на 30 градусов ПРОТИВ часовой стрелке, то вторая линия будет иметь градус пересечения с осью абсцисс 30+56.309932474019 = 86.309932474019 градусов
Тогда мы можем посчитать любым способом уравнение второй прямой
line_p xa=-2;ya=-8;f=86.309932474019
Параметры прямой линии по заданным параметрам
Общее уравнение Ax+By+C = 0
Коэффициент А = 23.011106998916
Коэффициент B = -1.4840558255286
Коэффициент C = 34.149767393603
Уравнение прямой в отрезках x/a+y/b = 1
Коэффициент a= -1.4840558255286
Коэффициент b = 23.011106998916
Уравнение прямой c угловым коэфициентом y = kx + b
Коэффициент k = 15.505553499458
Угол наклона к оси ( в градусах) f = 86.309932474019
Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0
Коэффициент p = -1.4809790664999
Коэффициент q = 3.0771888256405
Расстояние между точками=23.058912962428
Расстояние от точки до прямой li =
то есть наше уравнение второй линии есть y=15.505553499458x+23.011106998916
Проверим??
узнаем угол пересечения двух прямы х что мы нашли y=15.505553499458x+23.011106998916 и y=1.5x-5.5
line_p k=15.505553499458;b=23.011106998916,k=1.5;b=-5.5
Уравнение первой прямой
y = 15.505553499458 x + ( 23.011106998916 )
Уравнение второй прямой
y = 1.5 x + ( -5.5 )
Угол пересечения двух прямых(в градусах)
-29.999999999998
Точка пересечения двух прямых
x = -2.0357001242414
y = -8.553550186362
Как видно угол межуд прямыми именно такой какой нам задали в задании.
Задача решена.
Да, аналогично можно посчитать уравнение прямой которое было бы повернуто на 30 градусов по часовой стрелке
