| Первый многочлен |
![Исходный многочлен]() |
| Второй многочлен |
![Исходный многочлен]() |
| Остатки от деления двух полиномов |
|
Рассматривается вычисление наибольшего общего делителя (НОД) двух многочленов. Принцип который используется, такой же как и для нахождения НОД обычных чисел.
Отличие нашего калькулятора в том, что
1. Он показывает промежуточные остатки при вычислении
2. Многочлены могут быть комплексными, то есть содержать мнимые числа.
Теории больше не будет, и сразу перейдем к примерам вычисления, и вы поймете, как это вычисляется.
Найти НОД двух многочленов
 = x^{5}+x^{4}-4*x^{3}+5*x)
и
 = 2*x^{3}-x^{2}-2*x+2)
Сначала выбираем тот полином у которого степень выше и коэффицент при этой степени наибольший.
Делим один на другой f(x) на g(x). Можно делать это руками а можно воспользоваться калькулятором деления многочлена на многочлен.
Получаем остаток
*x^{2}+(0.5)*x+(3.5))
Теперь делим уже g(x) на полученный остаток
получаем
*x+(1.1358024691358))
Еще раз проделываем процедуру
получаем остаток
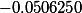
Если мы еще раз проведем такую же процедуру то получим в остатке ноль.
Закончили деление и смотрим на результат.
Предпоследнее значение от деления двух многочленов и есть значение НОД.
То есть наш ответ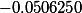
Кто хочет получить результат в виде дроби то стоит обратить внимание на Непрерывные, цепные дроби онлайн которая нам это значение в виде дроби и окончательный красивый ответ есть
НОД двух функций
и
равен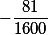 
Как же пользоватся ботом?
Выписыаем коэффициенты полиномов в строку разделяя их пробелом.
Получили
1 1 -4 0 5 это у нас первый полином
2 -1 -2 2 а это второй
Вводим их в соответсвующие поля и нажимаем рассчитать.
Смотрим результат
|
Первый многочлен |
%20=%20x^{4}+(1)*x^{3}+(-4)*x^{2}+(5)) |
|
Второй многочлен |
%20=%20(2)*x^{3}+(-1)*x^{2}+(-2)*x+(2)) |
|
Остатки от деления двух полиномов |
|
|
То есть всё то что мы делали руками.
Замечание: Как видно, в остаток всегда "примешивается" какая то мелкая погрешность. Это надо учитывать, в окончательном оформлении своего решения.Но это не всегда так. Если коэффициенты при старших степенях полиномов на любом этапе вычислений равны единицы, то погрешность результата нулевая.
Попробуем найти НОД комплексных многочленов
Пишем любые коэффициенты с мнимыми значениями и получаем
|
Первый многочлен |
%20=%20x^{6}+(1)*x^{5}+(i)*x^{4}+(i)*x^{3}+(i)) |
|
Второй многочлен |
%20=%20x^{2}+(-i)*x+(i)) |
|
Остатки от деления двух полиномов |
|
|
Еще один пример, с "нюансом"
|
Первый многочлен |
%20=%20x^{6}+(-4)*x^{5}+(2)*x^{4}+(5)*x^{3}+(2)*x^{2}+(-4)*x+(-8)) |
|
Второй многочлен |
%20=%20x^{5}+(-1)*x^{4}+(-1)*x^{3}+(1)*x^{2}+(-4)*x+(-4)) |
|
Остатки от деления двух полиномов |
|
|
Смотрите!! НОД не равен )
так как на предыдущей строке, уже получается ноль, правда с погрешность после 11 знака после запятой, но мы то с Вами понимаем (!!!) что это все равно ноль.
И наш правильный ответ *x^{2}+(1008)*x+(2016))
или вынеся за скобку общий множитель получаем что НОД равен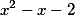 
Да, некоторые возразят "Ну, тут еще и думать надо.." Хотелось бы возразить, но не буду, так как согласен с ними что "Думать надо!"
Надеюсь, Ваши расчеты стали еще проще и быстрее!
*x^{3}+(-1)*x^{2}+(-2)*x+(2))
)
*x+(i))
*x+(1-1i))
)
*x^{4}+(-1)*x^{3}+(1)*x^{2}+(-4)*x+(-4))
*x^{2}+(-12)*x+(-20))
*x+(7.3999473215736E-11))
