| Исходные данные Xi=Yi |
|
| По заданным параметрам рассчитана эмпирическое уравнение регрессии |
![Регрессионная формула]() |
Как мы уже заметили в предыдущй
статье, данные, которые мы получаем в результатае наблюдений за какими то процессами, можно с достаточно низкой погрешностью представить в виде какой либо кривой. В этой статье мы рассмотрим регрессионный анализ, выражаемый параболой третьего порядка.
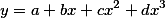
где a,b,c,d- неизвестные коэффициенты которые и надо найти, при известных измерениях Y и X
можно решать матричным способом, но есть уже рассчитанные формулы, которыми мы и воспользуемся
n - число членов ряда регресии
y - значения переменной Y
x - значения переменной X
Если вы будете пользоваться этим ботом через XMPP клиента, то синаксис такой
regress ряд X;ряд Y;2
где 2 - показывает что регрессию рассчитываем как нелинейную в виде параболы второго порядка
Что ж, пора проверить наши расчеты.
Итак есть таблица
|
X |
Y |
|
5 |
78.0 |
|
6 |
76.1 |
|
7 |
73.6 |
|
8 |
72.9 |
|
9 |
70.8 |
|
10 |
69.4 |
|
11 |
69.3 |
|
12 |
69.0 |
|
13 |
69.1 |
надо определить коэффиценты a, b, c,d
Не смотря на то, что есть функция regress для пользователей XMPP клиентов , нам удобнее вводить данные через WEB интерфейс.
В результате получим ответ
Удачных расчетов!
^4}-\sum{(x-x_s)^2}\sum{y(x-x_s)^2})
y\sum{(x-x_s)^5}-\sum{(x-x_s)^4}\sum{(x-x_s)^3y}))
^2y}-\sum{(x-x_s)^2}\sum{y})
^2}\sum{(x-x_s)^3y}-\sum{(x-x_s)^4}\sum{(x-x_s)y})
^4}-(\sum{(x-x_s)^2})^2)
^2}\sum{(x-x_s)^5}-(\sum{(x-x_s)^4})^2)
