| Заданная точка с координатами (X+Yi) |
![координаты точки]() |
| Заданная прямая |
![прямая]() |
| Координаты зеркальной точки |
![координаты результирующей точки]() |
Рассматривается расчет новых координат заданной точки или точек, зеркально отображенных относительно какой либо заданной прямой.
Алгоритм нахождения координаты зеркальной точки очень прост
1. Определяем точку пересечения оси абсцисс и прямой
2. Относительно этой точки делаем поворот на угол, равный угловому коэффициенту прямой.
Как это делается можно ознакомится в материале поворот точек на произвольный угол
3. С помощью матрицы вида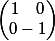 
, получаем зеркальное отображение точки относительно оси абсцисс.
4. Делаем обратный поворот (как в пункте 2)
5. Получаем результат.
Математически, решение поставленной задачи есть произведение трех матриц, в случае если точка, вокруг которой делается поворот, находится в начале координат
 & sin(\phi) \\ sin(\phi) & -cos(\phi) \end{pmatrix}*\begin{pmatrix} cos(\phi) & sin(\phi) \\ -sin(\phi) & cos(\phi) \end{pmatrix})
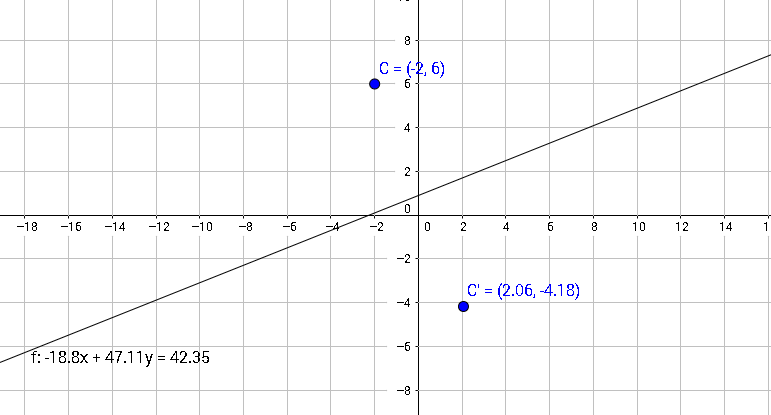
Рассмотрим реализацию этого алгоритма на примере, которой отбражен на рисунке выше.
Итак, у нас есть точка с координатами C(-2,6) и уравнение прямой -18.8x+47.11-42.35=0
Ввводим данные
Координаты точки С записываем вот в таком виде -2+6i
Коэффициенты прямой записываем через пробел -18.8 47.11 -42.35
Получаем ответ
|
Заданная точка с координатами (X:Y) |
 |
|
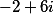Заданная прямая |
*y+(-42.35)=0) |
|
Координаты зеркальной точки |
 |
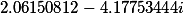Как видите это совпадает с графиком в начале статьи, сделанной с помощью geoGebra.
Удачных расчетов!!
