Каноническое уравнение эллипса по двум точкам

Две точки с координатами

Первая координата

Вторая координата

Каноническое уравнение эллипса

Большая полуось эллипса

Малая полуось эллипса

Эксцентриситет эллипса

Фокусное/фокальное расстояние

Коэффициент сжатия

Координаты первого фокуса F1(x1:y1)

Координаты второго фокуса F2(x2:y2)

Фокальный параметр

Перифокусное расстояние

Апофокусное расстояние

Уравнение эллипса в каноническом виде имеет вот такой вид.

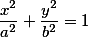
$?\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.

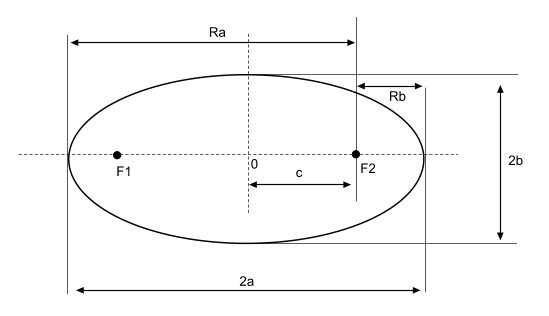
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.

Кроме этого, на этой странице мы получим следующую информацию.

Фокальный параметр - половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса

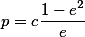
$p=c\frac{1-e^2}{e}$

Значение полуосей - большая полуось $a$ и малая полуось $b$ ( Естественно это в том случае, когда эллипс вытянут вдоль оси абсцисс)

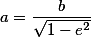
$a=\frac{b}{\sqrt{1-e^2}}$

Эксцентриситет - коэффициент, показывающий насколько его фигура отличается от окружности

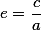
$e=\frac{c}{a}$

Фокальное расстояние

$c=ae$

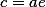
Коэффициент сжатия - отношение длин малой и большой полуосей

Перифокусное расстояние

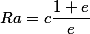
$Ra=c\frac{1+e}{e}$

Апофокусное расстояние

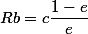
$Rb=c\frac{1-e}{e}$

Примеры задач

Cоставить каноническое уравнение эллипса по двум точкам $Ra=c\frac{1+e}{e}$

Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt

и получаем результат

Каноническое уравнение эллипса

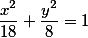$Введенное выражение$

Большая полуось эллипса

8.48528137423857

Малая полуось эллипса

5.656854249492381

Эксцентриситет эллипса

0.8958064164776166

Фокусное/фокальное расстояние

32.2490309931942

Коэффициент сжатия

0.4444444444444444

Координаты первого фокуса F1(x1:y1)

-16.1245154965971 : 0

Координаты второго фокуса F2(x2:y2)

16.1245154965971 : 0

Фокальный параметр

3.5555555555555554

Перифокусное расстояние

1.875484503402901

Апофокусное расстояние

34.1245154965971

И еще один пример

Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.

Если мы введем данные в калькулятор получим

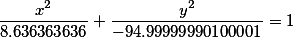$Введенное выражение$

Большая полуось эллипса

5.877538136328849

Малая полуось эллипса

NaN

Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.

Таким образом по этим двум точкам, нельзя построить эллипс.

А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.

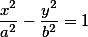
$frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам

Удачных расчетов!

Поиск по сайту