| Матрица инцидентности графа |
![Графическое представление ненаправленного графа]() |
| В виде строки |
|
Матрица инцидентности
В различных областях иногда нужно определять взаимосвязи между различными объектами. Связи между производствами, между денежными потоками и источниками этих денег, между сотрудниками для определения наиболее оптимальных психологических объединений, или для построения генеалогического древа.
Такие взаимосвязи можно представить в виде сети или графов.
Теория графов проникла во сферы жизни. Мы же, кроме матрицы инцидентности, графы будем использовать в различных ботах, таких как расчет произвольной площади по длинам и расчет электрических сетей, а также в других решениях которые будут реализованы.
Граф может рассматриваться как упорядоченное множество. Для наглядности элементы этого множества можно изобразить в виде точек, а связи между ними—в виде направленных (или ненаправленных) отрезков (называемых «ребрами»), связывающих эти точки. Мы говорим тогда о наглядно-геометрическом представлении графов. При этом важно лишь то, какие точки связаны друг с другом, длина же связующих отрезков не принимается во внимание. Этим способом можно описывать отношения, которые могут иметь место в жизни, например "необходимо для" , "в связи с", "зависит от" и тому подобное.
Даны два множества: множество узловых точек А и множество ребер Б. Если между двумя узловми точками А1 и А2 существует ребро Б1, то говорят что ребро Б1 инцидентно узловым точкам А1 и А2. Таким образом, между элементами из А и Б устанавливаются отношения инцидентности.
При переводе графа в матричную форму нужно соблюдать следующие правила.
Если существует ребро, ведущее из точки А в точку Б, то элемент матрицы АБ полагается равным 1, если же точки А и Б не связаны, то АБ = 0. При этом полагается, что ни одна точка не соединена сама с собой.
Таким образом мы получаем квадратную матрицу, которая называется матрицей инцидентности графа.
Хотелось бы заметить что в интернете много определений инцидентности, и в каждом примере используется почему то какой то свой особенный алгоритм, и матрицы у всех получаются различные. Мы взяли для расчета матрицы информацию из книги Гильберт А. "Как работать с матрицами". 1977 года издания.
При вводе данных наш бот не просит названия ребер. Он основывается на данных об узловых точках: какая точка и какие соседние точки доступны.
Синтаксис
Jabber: graf выражение
WEB: выражение
где,
Выражение - строка, определяющая соответствие связей между узловыми точками, разделенная точкой с запятой.
A(B,C);C(F,A) и так далее
Примеры
Рассмотрим наш граф
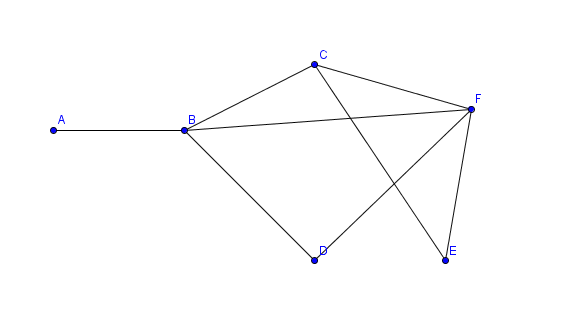
Пишем
A связан только с B
B связан с точками C A D и F
ну и так далее. Смысл я надеюсь понятен.
и окончательный запрос будет таким A(B);B(A,C,D,F);C(B,F,E);D(B,F);E(C,F);F(C,E)
Запрос избыточен, так как видно что некоторые ребра записаны дважды, но это не беда.
Сделано именно для упрощения ввода, что бы "не думалось" какие ребра вы ввели а какие еще нет.
И получаем следующий результат - это и будет матрицей инцидентности.
Если же Вам нужна обратная задача - по матрице смежности построить граф, то Вам стоит обратится вот сюда Построить граф по матрице
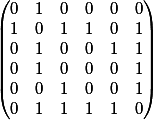
Теперь Вы, основываясь на этой матрице можете легко, определять связи между элементами.