| Заданная матрица смежности ненаправленного графа |
![Матрица смежности]() |
| Полученный граф, построенный по матрице |
![По матрице созданный граф]() |
Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г.
Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками.
Однако дальнейшее развитие математики и особенно ее приложений дало сильный толчок развитию теории графов.
Уже в XIX столетии графы использовались при построении схем электрических цепей и молекулярных схем.
Граф - это одно из представлений связей, между объектами / событиями.
В настоящее время теория графов находит многочисленные применения в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сети нефтепроводов и вообще в так называемом «программировании». Теория графов теперь применяется и в таких областях, как экономика, психология и биология.
В виде графов преобразовываются электрические схемы, производственные цепочки на предприятии, план мероприятий, оптимальная логистическая доставка, связи между родственниками, друзьями и многое другое.
Графы делятся на ненаправленные, направленные, с весовыми коэффициентами(взвешенные) и без коэффициентов.
Каждый граф имеет определенные характеристики. Основные из них это остов графа, матрица смежности, матрица инцидентности.
Остов графа - это подграф данного графа, содержащий все его вершины и являющийся деревом.
Матрица смежности графа - это квадратная матрица ( по числу вершин графа) где, каждый элемент матрицы (на пересечении i- столбца и j-ряда) есть состояния связи между вершинами i и j.
Элемент матрицы равен 1 если i-вершина графа, соединена с j-вершиной графа.
Во всех других случаях, в том числе когда i=j, значение элемента матрицы равно 0.
Это условие применимо только для ненаправленных графов и только для связей которые не начинаются и заканчиваются на одной и той же вершине ( петля)
Ненаправленный граф - граф, где не указаны направления движения связей между любыми вершинами.
Невзвешенный граф - граф, где связям между любыми вершинами не присвоено никакое значение, а показывает только лишь сам факт связи этих двух вершин
На этой странице бот строит ненаправленный граф, если для него задана матрица смежности.
Если мы не можете в уме построить матрицу смежности, то для этого есть ресурс Теория графов. Матрица смежности онлайн где можно построить такую матрицу.
Интересные особенности
В матрице смежности неориентированного графа (взвешенного или невзвешенного) не важно, есть одна очень важная особенность
Значения матрицы относительно главной диагонали - одинаковы.
Таким образом в принципе достаточно в качестве исходных данных вводить только верхнюю(диагональную) часть матрицы, но для удобства восприятия, ввод данных был сделан для полной матрицы.
Второй вывод который следует из вышесказанного следующий( и в примерах он прослеживается): Бот не проверяет симметричность-соответствие данных в позициях матрицы относительно главной диагонали.
Примеры:
Задана матрица смежности такого вида
\(\begin{pmatrix}0&0&1&0\\1&0&1&0\\0&0&1&1\\0&1&0&0\end{pmatrix}\)
В запросе пишем 0 0 1 0 1 0 1 0 0 0 1 1 0 1 0 0
и получаем ответ
| Заданная матрица смежности ненаправленного графа |
| \(\begin{pmatrix}0&0&1&0\\1&0&1&0\\0&0&1&1\\0&1&0&0\end{pmatrix}\) |
| Полученный граф, построенный по матрице |
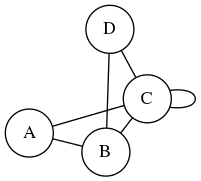 |
Удачи в расчетах!!