| Вы ввели следующее выражение |
![Введенное выражение]() |
| Окончательный результат выражения |
|
Обновление: На 12 сентября 2017 года, упрощен ввод данных. Теперь можно вводить выражение без знака умножения. Например 3(2+i)(-4+sin(i)). Если заметили неправильный расчет, просьба внизу страницы обозначить ошибку в виде комментария. Спасибо!
Позволяет высчитывать результат произвольного комплексного выражения с любым количеством скобок, любой длины и с любыми числами (как действительными, так и мнимыми)
Арифметическое выражение подразумевает собой выражение, которое использует 4 основных операции: умножение, деление, сложение и вычитание.
Напомним как производятся эти операции:
Сложение двух комплексных чисел
+(c+di)=(a+c)+i(b+d))
Вычитание двух комплексных чисел
-(c+di)=(a-c)+i(b-d))
Умножение двух комплексных чисел
*(c+di)=(a*c-b*d)+i(b*c+a*d))
Деление двух комплексных чисел
\(\cfrac{(a+bi)}{(c+di)}=\cfrac{(a*c+b*d)}{c^2+d^2}+i\cfrac{(b*c-a*d)}{c^2+d^2}\)
Данный бот еще может использовать пятую операцию - возведение в степень, а так же все основные тригонометрические функции (синус, косинус, тангенс), обратные тригонометрические функции, взятие логарифма и экспоненты.
Заметьте, эти функции могут использовать как действительные аргументы, так и комплексные, что открывает широкие возможности по вычислению выражений.
Возведение в степень осуществляется по известной формуле Муавра. Степень числа, может быть как действительным так и мнимым.
Калькулятор работает, исправен, и не допускает ошибки при корректном вводе выражения.
Как уже было сказано, выражение по сложности может быть неограниченным по размерам и иметь множество скобок.
Синтаксис
Если используете Jabber или любой другой XMPP клиент: calc_i <строка>
Если используете данный сайт: <строка>
Строкой может быть любое выражение без каких либо функций. Могут воспользоватся следующие операции:
+ сложение
- вычитание
* умножение
/ деление
^ возведение в степень
синус(sin)
косинус(cos)
натуральный логарифм(ln)
тангенс(tan)
артангенс(atan)
арксинус(asin)
арккосинус(acos)
гиперболический синус(sinh)
гиперболический косинус(cosh)
гиперболический тангенс(tanh)
Число в выражении может быть как действительным, которое записывается в привычном виде, так и комплексным числом которое обозначается символом i
Просьба по возможности оборачивать каждое комплексное число в круглые скобки, если первый символ в нём является минус (-)
Примеры
(-4-1i)/((-5-2i)+7-1.2i)
или в более наглядном виде
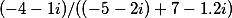
Получаем
Наш запрос выглядит так как мы его и сформировали в самом начале
calc_i (-4-1i)/((-5-2i)+7-1.2i)
Результат выражения
Действительная часть -0.33707865168539
Мнимая часть -1.0393258426966
i/(5-i)+(-4+2.7i)/(3-i)/0.2i
Получаем
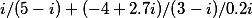
Наш запрос выглядит так
calc_i (i/(5-i))^2+(-4+2.7i)/(3-i)/0.2i
Результат выражения
Действительная часть 2.0115384615385
Мнимая часть 7.5423076923077
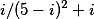
Запрос calc_i i/((5-i)^2)+i
Результат выражения
Действительная часть -0.01479289940828
Мнимая часть 1.0355029585799
Запрос atan(i+2)-cos(1+i/(3-i))^(2*i^(1/2))
Результат выражения
Действительная часть 0.66468285388895
Мнимая часть 1.0051451851734
Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа.