| Исходный многочлен |
![Корни многочлена]() |
| Кубическая резольвента |
![Корни многочлена]() |
| Корни кубической резольвенты |
![Корни многочлена]() |
![Корни многочлена]() |
![Корни многочлена]() |
| Корни заданного многочлена 4 степени |
![Корни многочлена]() |
![Корни многочлена]() |
![Корни многочлена]() |
![Корни многочлена]() |
| Вспомогательные коэффициенты |
F2=![Параметр F2]() |
F1=![Параметр F1]() |
T=![Параметр T]() |
Данный калькулятор позволяет высчитывать корни произвольного полинома четвертой степени. Коэффициенты могут быть как вещественными так и комплексными числами.
Использовалась определенная методика, которая нигде не описана и не разобрана.
Формулами Феррари не стал пользоваться - не интересно.
Несмотря на свой собственный путь, все равно утыкаешься в задачу решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты.
И по всей видимости избежать её никак не получится.
Но дальше все идет по другому.
По любому значения корня резольвенты, мы высчитываем три вспомогательный параметра.
Зная эти три параметра, мы можем легко найти все четыре корня исходного уравнения.
Есть только один нюанс с которым сталкивались предшественники, мне тоже надо иногда каким то определять знак + или - для одного вспомогательного параметра.
Теперь в виде формул
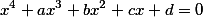
Заменой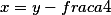 
мы получаем так называемый приведенный многочлен
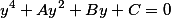
Решение данного уравнения ищем в виде сумм двух функций
+F(T,F_2))
Три вспомогательных параметра связаны к коэффициентами приведенного полинома через следующие соотношения
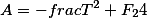
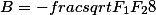
^2-frac{F_1}{2}}{64})
Выражая любой из вспомогательных параметров мы получаем, в том или ином виде кубическую резольвенту
Например, если выразим F2
=8B^2)
Это кубическое уравнение которое подстановкой 
превращается к классическую кубическую резольвенту.
Теперь о нюансе о котором говорил раньше. Какой же знак брать когда высчитываем корни?
Критерий оказывается очень простой. Берем любой корень резольвенты и сравниваем его
)
если это условие верное то ставится +(плюс), если условие неверное то -(минус)
Дальше все эти параметры подставляются в формулу
и определяются корни уравнения 4 степени.
Еще хотелось бы поговорить про критерий. Вдумчивый читатель спросит: "А что если любой корень резольвенты является комплексным числом? Какой в этом случае критерий?"
Лучшим способом, я посчитал для подстановка корня в исходное уравнение. Для этого есть простой алогритический способ описанный в статье Значение производной многочлена по методу Горнера. Если выражение обращается в ноль, то есть является верным, то знак не меняется. Если иначе то знак ставим минус.
Решать комплексные уравнения 4 степени теперь можно достаточно легко и быстро. В онлайн сервисах Вы такого не найдете.
Попробуйте решить уравнение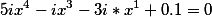 
Один из корней равен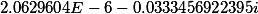 
Кто считает что действительной частью можно принебречь и отбросить как "почти ноль" глубоко ошибается. Отбросив его у нас значение функции будет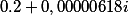 
, а не ноль.
И только с учетом "такой маленькой" действительной части уравнение становиться тождественным.
Поэтому точность в вычислениях очень важны.
Если Вы вдруг заметили ошибку в расчетах ( а вдруг?) , просьба сообщить. Но я надеюсь, что такого не произойдет.
Несколько примеров:
| Исходный многочлен |
*x^3+(-9i)*x^2+(-4)*x^1+(-10i)) |
| Кубическая резольвента |
*x^2+(2620+2464i)*x^1+(-18432-34560i)) |
| Корни кубической резольвенты |
 |
 |
 |
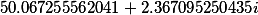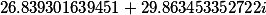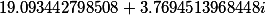| Корни заданного многочлена 4 степени |
 |
 |
 |
 |
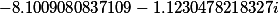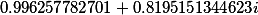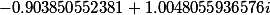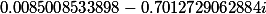| Вспомогательные коэффициенты |
| F2= |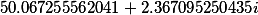
F1= |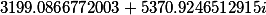
T= |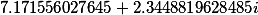
| Исходный многочлен |
*x^3+(-4)*x^2+(-20)*x^1+(-5)) |
| Кубическая резольвента |
*x^2+(272)*x^1+(-128)) |
| Корни кубической резольвенты |
 |
 |
 |
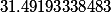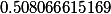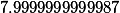| Корни заданного многочлена 4 степени |
 |
 |
 |
 |
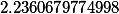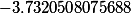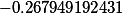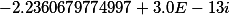| Вспомогательные коэффициенты |
| F2= |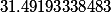
F1= |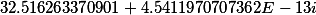
T= |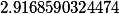
