Функция ошибок

Аргумент функции ошибок erf(x)

Функция ошибок

Дополнительная функция ошибок

Функция ошибок, она же функция Лапласа, он же интеграл вероятности - все это одна и та же сущность, которая выражается функцией

$\operatorname {erf}\,x={\frac {2}{{\sqrt {\pi }}}}\int \limits _{0}^{x}e^{{-t^{2}}}\,{\mathrm d}t$

и используется в статистике и теории вероятностей.

Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.

Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией

$\operatorname {erf}\,x=1-{\frac {\Gamma \left({\frac {1}{2}},x^{2}\right)}{{\sqrt \pi }}}$

Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую 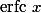$\operatorname {erfc} \,x$ (иногда применяется обозначение 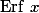$\operatorname {Erf} \,x$ ) и определяется через функцию ошибок:

$\operatorname {erfc}\,x=1-\operatorname {erf}\,x={\frac {2}{{\sqrt {\pi }}}}\int \limits _{x}^{{\infty }}e^{{-t^{2}}}\,{\mathrm d}t$

В приницпе это все, что можно сказать о ней.

Калькулятор высчитывает результат как в вещественном так и комплексном поле.

Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.

Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.

Несколько примеров:

Функция ошибок

$Результат расчета функции Лапласа$