| По заданным точкам построен полином |
![Исходный многочлен]() |
Задача, которую решает этот калькулятор, звучит так: Построить по N -известным значениям полином N-1 степени.
Это является одним из видов аппроксимации, но практически, редко используется. Связанно это с тем, что несмотря на то что в узловых точках (исходных) значение вычсленного полинома совпадает на 100%, в промежуточных точках значение может быть очень далеким от реальных значений.
Простой пример это показывает. Пусть какому то ученому пришла в голову рассчитать аппроксимирующий полином, который показывал бы как растет человек год от года.
Он запросил данные и получил, что в первый год рост человека 50см, на 3 год - 80 см, в 6 лет -120см, в 15 лет -150 см, а в 25 лет - 180 см
Введя данные он получил следующий полином
|
По заданным точкам построен полином |
%20=%20(0.0030331510594691)*x^{4}+(-0.11154306220018)*x^{3}+(0.5606772613291)*x^{2}+(14.086024720879)*x+(35.461807928933)) |
Вроде бы все хорошо, в каждой контрольной точке, значения совпадают, но если мы посмотрим график...
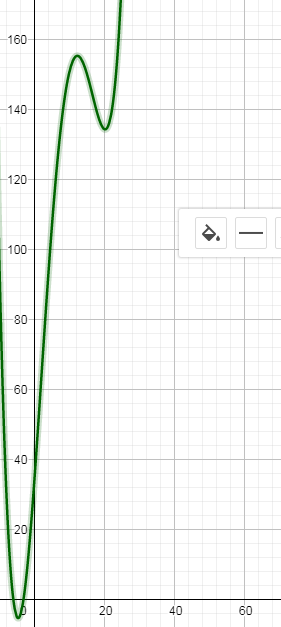
Удивительно, но где то в 20 лет у человека рост резко уменьшается до 130 см.
Мы то с Вами прекрасно понимаем, что это не так, но в других расчетах, такая аппроксимация может приводить вот к таким "аномалиям" и следовательно к неверным выводам.
Для чего же тогда нужен этот калькулятор?
Если мы знаем(!) что наша неизвестная функция есть многочлен какой то степени, то взяв необходимое количество точек, мы всегда с высокой точностью определим эти коэффициенты.
Несколько примеров:
Я хочу определить какой многочлен поможет найти зависимость, от следующих значений, если при
1 результат