Введение
Самые первые тригонометрические функции, которые встречаются у нас в жизни, имеют название - синус и косинус.
Одно из определений в современном мире: Синус это отношение противолежащего катета прямоугольного треугольника к его гипотенузе.
Обозначение синуса -
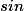
Особенности и факты
1. Синус нуля равен нулю. Несмотря на такой банальный факт, именно это правило поможет запомнить что синус это отношение именно противолежащего катета, а не прилежащего. Как?
На данном графике показан как раз синус угла CAD как отношение стороны CD к AC
Двигаясь по окружности в правую сторону, мы заметим, что отрезок CD становится все меньше и в конечном итоге, мы можем получить что отрезок CD становится равным нулю. А отношение нуля к какому либо числу равно также нулю. В этом случае несложно убедится что угол, который на рисунке равен 34.23 градуса, становится все меньше и также превращается в нуль.
Таким образом мы и получили что
2. Синус 90 градусов равен единице. Рассуждая аналогично и смотря на выше приведенный рисунок, видим, что двигая точку С по окружности влевую сторону, точка в какой то момент пересечет ось ординат. В этот момент, гипотенуза прямоугольного треугольника будет равна прилежащему катету, а их отношение равно единице.
Угол, образованный между точками
B, началом координат и точкой
C будет равен прямому углу то есть 90 градусов. Или, если переводить в радианы то
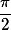
Формулы расчета синуса угла можно представить в различных видах:
1. В виде ряда
=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-\cdots = \sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{(2n+1)!})
2. В виде комплексного выражения =\frac{e^{xi}-e^{-xi}}{2i})
3. В виде косинуса ^2+cos(x)^2=1)
Это основные формулы, которые желательно знать.
Арксинус(asin) - есть функция обратная функции синуса(sin).
То есть
Данный бот рассчитывает произвольное выражение синуса. В том числе, если синус будет иметь комплексное выражение.
Примеры
sin(1+i)
Пишем в строке запроса 1+i
и получаем что
=1.298457581416+0.63496391478474i)
Узнать арксинус комплексного выражения следующего вида (i+5)/cos(i/3+1)-ln(0.5-i)
Пишем строке запроса эту функцию и получаем
}{cos(\frac{i}{3}+1)}-ln(0.5-i))=0.79649172695434+2.8488065958421i)