Уравнение Ферхюльста
| Исходные данные Xi=Yi |
|
| По заданным параметрам рассчитана эмпирическое уравнение регрессии |
![Регрессионная формула]() |
В жизни, при развитии того или иного объекта в замкнутом пространстве, всю жизнь его можно в большинстве случаев свести к следующим этапам.
1. начальное развитие
2. бурный рост
3. замедление роста и переход в равновесное состояние
По такому плану развиваются все живые существа в замкнутой областе/ареале при наличии достаточной пищи.
Кривая, которая показывает динамику изменения таких сообществ называется логистической кривой.
Графически подобная кривая выражается с помощью уравнения которое получило название Ферхюльста
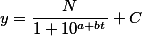
где y- учитываемый признак
t-время,прошедшее от начальной, или базисной(C) величины признака, с которой начато его измерение, до предельной в данных условиях величины N, котрой он достиг за время t.
a,b- параметры уравнения, определяющие характер логистической кривой.
Путем логарифмического преобразования это уравнение приобретает следующее выражение:
Обозначив
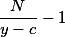
через
z, получаем уравнение линейной регрессии:
Что бы решить её, нам потребуется решить систему уравнений
Решая эту систему относительно параметров a и b, получаем следующие формулы:
n - число членов ряда регресии
y - значения переменной Y
t - значения переменной X
Если вы будете пользоваться этим ботом через XMPP клиента, то синаксис такой
regress ряд X;ряд Y;6
где 6 - показывает, что регрессию считаем как логистическую кривую.
Что ж, пора проверить наши расчеты.
Итак есть таблица
|
t |
y |
|
0 |
5 |
|
1 |
20 |
|
2 |
100 |
|
3 |
300 |
|
4 |
350 |
|
5 |
380 |
|
6 |
385 |
|
7 |
389 |
надо определить коэффиценты a, b
Удачных расчетов!
=a+bt)
=a+bt)
}=an+b\sum{t}\\\\\sum{tlg(z)}=a\sum{t}+b\sum{t^2})
}}\sum{t^2}-\sum{t}\sum{tlg(z)}))
}-\sum{t}\sum{lg(z)}))
^2)
