| Вычисленные координаты заданной фигуры |
|
| Площадь заданного многоугольника (в условных единицах) |
|
Определение площади произвольной фигуры состоящей из прямых, построенная в декартовых координатах, задача простая. Это реализовано у нас на сайте в материале площадь многоугольника по координатам.
Но что делать когда координатной сети нет, а площадь посчитать необходимо.
В этом материале я Вам расскажу как измерить площадь с помощью обычной линейки (рулетки, дальномера)
Читатели ответят "Но нас в школе учили что с помощью линейки, измеряя длины сторон площадь фигуры нельзя определить"
Например и левая и правая фигура имеют одинаковые длины сторон, но площадь у них явно разная
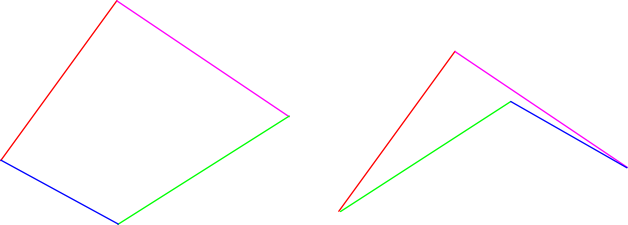
Действительно, приходится согласится с таким утверждением, но
во первых, мы не будем измерять длины сторон, они нам неинтересны, а измеряем длины только до вершин фигуры
во вторых, мы внесем дополнительное условие, мы будем делать два измерения с двух разных точек.
И второе условие является ключевым, которое и позволит нам узнать и стороны этой фигуры и площадь и даже координаты, если мы укажем какую точку считать за начало координат.
Пусть у нас есть вот такая фигура.
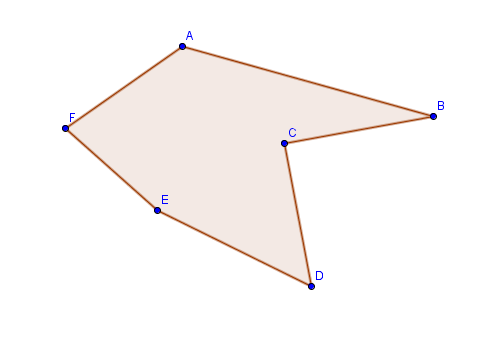
Сможете посчитать площадь? Есть конечно способ узнать с помощью палетки, накладывая её на фигуру и определяя количество полных квадратов, но такой способ все таки приближенный, во вторых к реальной жизни мало относиться, если представить что это не фигура у нас на столе, а дачный участок.
Решение нашей задачи состоит в следующем.
На первом этапе мы встаем например в точку А и измеряем расстояние до всех других точек.
На втором этапе мы встаем в точку С, и также измеряем расстояние до всех других точек.
Всё.. все измерения у нас завершены и теперь их надо обработать.
У нас есть расстояние до всех точек. Узнать параметры треугольника по трем сторонам не представляет трудности.
А если мы примем за начало координат первую точку где делали первое измерение, а вторая точка отложена по оси абсцисс, или ординат(для измерения площади это не принципиально) то зная параметры треугольника и координаты двух точек, легко высчитываем координату третьей точки.
Пробегая по всем точкам, мы получим их координаты, а как мы уже сказали выше, площадь по координатам мы считать умеем хорошо.
Применимость в жизни очень высокая, так как живем мы не в координатой системе Декарта, а все больше в векторной, так как посылая человека, Вы указываете ему не координаты типа "е2-е4", а показываете куда ему идти и как далеко.
Измерение площадей реальных фигур с помощью линейки, площадей участков с помощью дальномера - все это стало возможным с помощью этого калькулятора.
И заметьте! Ни одного измерения углов!
Рассмотрим пример. Узнать площадь звездочки.