| Вы ввели следующие координаты многоугольника |
![Введенное выражение]() |
| Площадь заданного многоугольника (в условных единицах) |
|
Калькулятор позволяет высчитывать по заданным координатам вершин площадь многоугольника (треугольника, трапеции, параллелограмма, пятиугольника и т.д) а также любых других непересекающихся многоугольников.
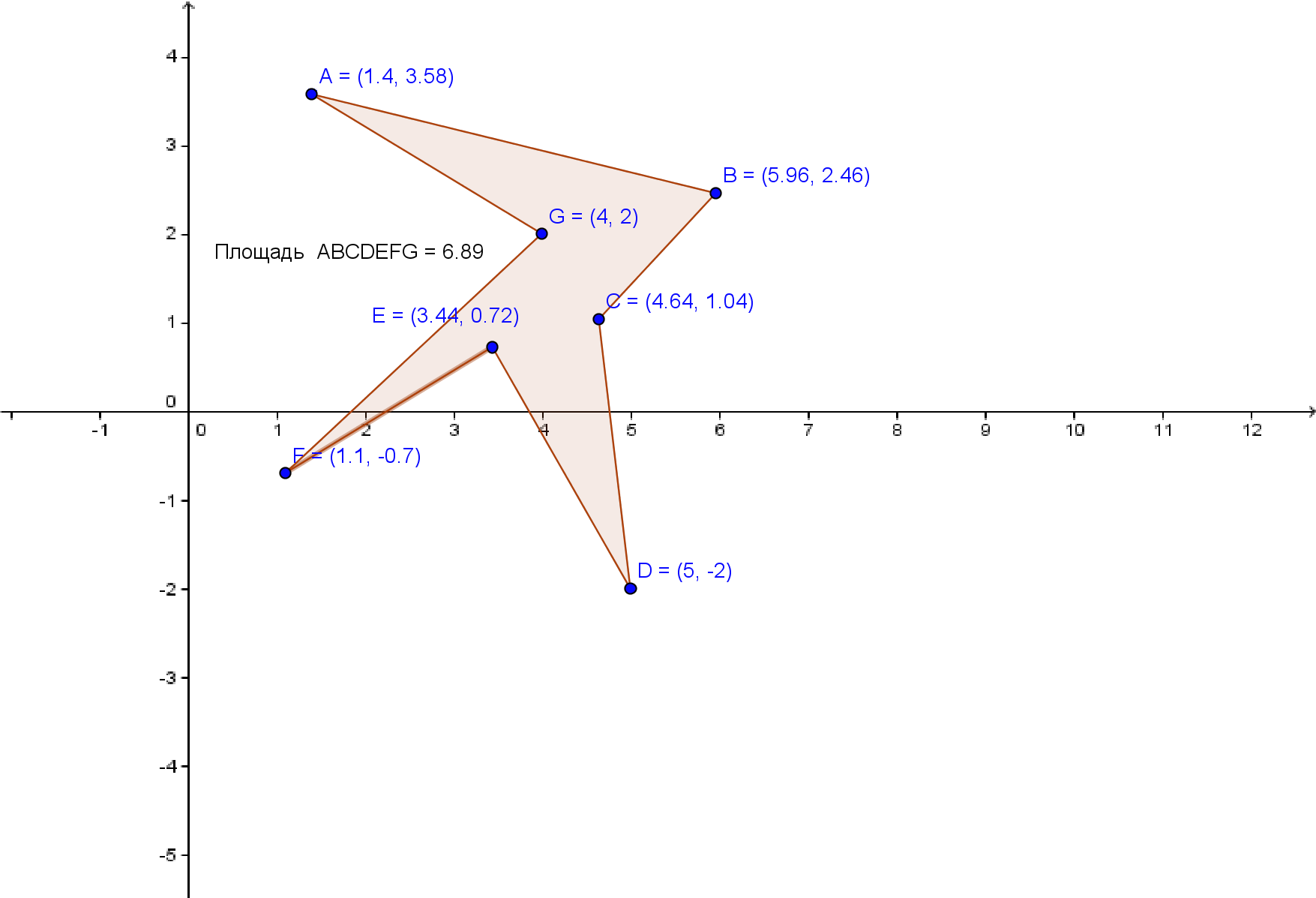
Используется метод трапеций, суть которого заключается в том, что многоугольник представляет собой сумму трапеций, две вершины из которого это две соседние вершины многоугольника, а две другие вершины трапеции, есть абсциссы координат двух вершин многоугольника.
Такой метод позволяет рассчитывать не только выпусклые многоугольники, но и любые другие, главное, что бы линии этого многоугольника не пересекались.
Есть еще два подобных сервиса: Площадь пересечения окружностей и Прямая линия
Кроме этого стоит обратить внимание на такие материалы как: Касательная к кривой второго порядка
Пересечение прямой и кривой второго порядка
Расчет кривых второго порядка на плоскости
Координаты вершин задаются в общей строке вида x1:y1 x2:y2 x3:y3 ....xn:yn
Координаты вершин являются действительные числа.
Координата каждой точки (абсцисса и ордината) записывается через двоеточие(без пробелов!)
Координаты вершин вводятся ПОСЛЕДОВАТЕЛЬНО по часовой или(!) против часовой стрелки.

Каждая координата вида x:y должен быть отделена пробелами от другой.
Нет никаких ограничений на количество координат вершин.
Примеры
mnog 5:7 9:7 10:2 2:2
Площадь многоугольника заданный координатами 5:7 9:7 10:2 2:2
равен 30
Возможно Вам будет интересно Узнать площадь фигуры линейкой или дальномером