| Матричная форма записи данной квадратичной формы |
![Результат умножения]() |
Расчет квадартичной формы достаточно простая задача, по крайней мере описательная часть примитивна до невозможности и алгоритм расчета, когда известна матрица, заключается в расчете каждого из элемента по формуле
\(Q(x)=\sum_{{i,j=1}}^{n}a_{{ij}}x_{i}x_{j}\)
где, 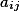 - элемент матрицы
- элемент матрицы
\(A=\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn}\end{pmatrix}\)
Но все примитивное, не значит удобное и при вычислении квадратичной формы легко ошибиться. Наш калькулятор поможет не делать ошибок в вычислениях.
Как и во всех калькуляторах, матрица может содержать не только вещественные числа, но и комплексные.
При вводе данных, у нас есть два поля:
первое, это матрица;
второе, это способ именования каждого из элемента.
Если мы во втором поле напишем какой то символ (a,b,c....) то каждый элемент будет именоваться 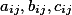
Рассмотрим несколько примеров.
Вводим элементы матрицы через пробел (можно каждую строку начинать с новой строки)
и получаем следующие результаты
\(\begin{pmatrix}x_{0}&x_{1}&x_{2}\\\end{pmatrix}*\begin{pmatrix}1&1&2\\1&3&0\\2&0&1\\\end{pmatrix}*\begin{pmatrix}x_{0}\\x_{1}\\x_{2}\\\end{pmatrix}=\\=(1)x_{0}^2+(2)x_{0}x_{1}+(4)x_{0}x_{2}+(3)x_{1}^2+(1)x_{2}^2\)
\(\begin{pmatrix}a_{0}&a_{1}&a_{2}\\\end{pmatrix}*\begin{pmatrix}2&2&-1\\2&-5&3\\-1&3&8\\\end{pmatrix}*\begin{pmatrix}a_{0}\\a_{1}\\a_{2}\\\end{pmatrix}=\\=(2)a_{0}^2+(4)a_{0}a_{1}+(-2)a_{0}a_{2}+(-5)a_{1}^2+(6)a_{1}a_{2}+(8)a_{2}^2\)
Расчет в комплексном поле
\(\begin{pmatrix}s_{0}&s_{1}&s_{2}&s_{3}\\\end{pmatrix}*\begin{pmatrix}i&4&2-i&-2\\-i&2&2-i&i+7\\2i-9&0.4-i&11&-6\\1&0&-i&2i\\\end{pmatrix}*\begin{pmatrix}s_{0}\\s_{1}\\s_{2}\\s_{3}\\\end{pmatrix}=\\=(i)s_{0}^2+(4-1i)s_{0}s_{1}+(-7+1i)s_{0}s_{2}+(-1)s_{0}s_{3}+(2)s_{1}^2+(2.4-2i)s_{1}s_{2}+(7+1i)s_{1}s_{3}+(11)s_{2}^2+(-6-1i)s_{2}s_{3}+(2i)s_{3}^2\)
Удачных расчетов!!