| Полный эллиптический интеграл 1 рода |
![Полный эллиптический интеграл 1 рода]() |
| Полный эллиптический интеграл 2 рода |
![Полный эллиптический интеграл 2 рода]() |
Эллиптические интегралы впервые появились при задаче определения периметра произвольного эллипса.
В общем случае эллиптическим называется интеграл
 dx )
где - рациональная функция от  и
и 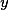 , а
, а 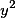 - многочлен третьей или четвертой степени от
- многочлен третьей или четвертой степени от 
Известны преобразования, позволяющие выразить любой эллиптический интеграл через интеграл от рациональной функции  и следующие три канонических интеграла.
и следующие три канонических интеграла.
Эллиптический интеграл первого рода
=\int_{0}^{\varphi} \frac{ dx }{sqrt{1-k^2sin^2(t)}})
Эллиптический интеграл второго рода
=\int_{0}^{\varphi} \sqrt{1-k^2sin^2(t)}dt)
Эллиптический интеграл третьего рода
 = \int \limits_{0}^{\varphi}\!\frac{d\varphi}{(1+n \sin^2 \varphi) \sqrt{1-k^2\sin^2\varphi}})
Здесь
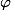 - амплитуда
- амплитуда
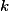 - модуль
- модуль
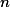 - параметр эллиптического интеграла(третьего рода)
- параметр эллиптического интеграла(третьего рода)
Интегралы, у которых амплитуда 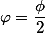 называются полными. Для интегралов первого и второго рода применяются соответственно обозначения.
называются полными. Для интегралов первого и второго рода применяются соответственно обозначения.
=F(\frac{\pi}{2},k))
=E(\frac{\pi}{2},k))
Используется также дополнительный модуль, равный по определению
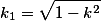
В таблицах эллиптических интегралов принято амплитуду выражать в градусах. Кроме того, часто величины 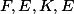 рассматриваются как функции модулярного угла - угла, заменяющего модуль и выраженного в градусах:
рассматриваются как функции модулярного угла - угла, заменяющего модуль и выраженного в градусах:
)
Таким образом
)
)
При вычислении 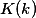 одним из наиболее эффективных является итерационный метод арифметическо-геометрического среднего (АГС). Начиная с пары
одним из наиболее эффективных является итерационный метод арифметическо-геометрического среднего (АГС). Начиная с пары 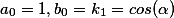 находятся следующие среднее арифметическое и среднее геометрическое, которые образуют две сближающиеся последовательности:
находятся следующие среднее арифметическое и среднее геометрическое, которые образуют две сближающиеся последовательности:
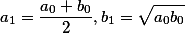
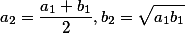
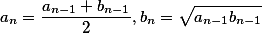
Процесс заканчивается при таком 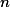 для которого
для которого  и
и  совпадают. Искомое значение
совпадают. Искомое значение 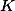 определяется по формуле
определяется по формуле
=\frac{\pi}{2a_n})
Есть еще более простая формула, при 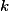 стремящегося к единице.
стремящегося к единице.
=ln(\frac{4}{k_1}))
Вычисление полного эллиптического интеграла второго рода производится по той же схеме что и в случае интеграла первого рода , с использованием разностей
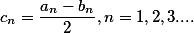
получаемой на каждой итерации. Тогда
=(1-\frac{1}{2}\sum_{n=0}^N2^nc_n^2)K(k))
где 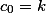
Бот, рассчитывает значения полного эллиптического интеграла первого и второго рода, при любых значениях 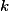
С помощью этого бота мы сможем легко определять периметр эллипса, а также длину дуги любой кривой второго порядка.
Некоторые примеры
При значении x=i
|
Полный эллиптический интеграл 1 рода |
%20=%201.3110287771461) |
|
Полный эллиптический интеграл 2 рода |
%20=%201.910098894514) |
Хотелось бы заметить, что если проверять по данным который дает сайт www.wolframalpha.com получается что у него другие значения. Это связано с тем, что на том сайте, аргумент предварительно возводится в квадрат, то есть там значения показаны для значения 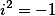
|
Полный эллиптический интеграл 1 рода |
%20=%201.6857503548126) |
|
Полный эллиптический интеграл 2 рода |
%20=%201.4674622093395) |
и еще один
|
Полный эллиптический интеграл 1 рода |
%20=%200.19712334640198-0.43443093218712i) |
|
Полный эллиптический интеграл 2 рода |
%20=%200.098367068970897+7.7518095000745i) |
Если Вы где то обнаружили ошибку в расчетах, убедительная просьба сообщить об этом. Спасибо!!!
Удачных расчетов!