Пересечение окружности и прямой.Координаты.

Элементы окружности или координаты

x^2+y^2+ x+ y+ =0

Элементы прямой линии

Уравнение окружности

Уравнение прямой к угловым коэффициентом

Координаты пересечения окружности и прямой

Рассмотрим более подробно задачу пересечения окружности и прямой. В принципе само решение есть уже в общем виде Пересечение прямой и кривой второго порядка, но мы рассмотрим и выведем формулы точек пересечения этих двух геометрических объектов.

Уравнение прямой, как мы знаем из материала Расчет параметров прямой линии по заданным параметрам могут быть заданы в нескольких видах:

- в общем виде,

- с угловым коэффициентом

- в нормальном виде

Что бы решить нашу первоначальную задачу, использовать будем уравнение прямой с угловым коэффициентом которое имеет вид

$y=kx+b$

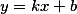
Уравнение окружности тоже может быть выражена в различных видах

Например в общем виде оно имеет вид

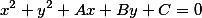
$x^2+y^2+Ax+By+C=0$

Подставим в уравнение окружности, уравнение прямой

$0=x^2+(kx+b)^2+Ax+By+C$

Раскроем скобки

$x^2+(kx)^2+2kbx+b^2+Ax+By+C=0$

Или

$x^2(1+k^2)+x(2kb+A+Bk)+b^2+Bb+C=0$

Мы получили стандартное квадратное уравнение, решив котрое мы получим два значения, которые и будут являтся абсциссами точек пересечения прямой и окружности.

Подставим эти координаты в уравнение прямой, мы получим две ординаты точек пересечения.

Таким образом решение найдено.

Для упрощения, для сверки результатов - калькулятор помогает Вам рассчитать эти точки. Интересная особенность состоит в том, что прямая может быть задана в любом виде, хоть виде двух точек.

А уравнение окружности может быть не только введено с помощью коэффицентов, но и в виде пары трех координат через которые, эта окружность будет проходить.

Поиск по сайту