Вычислить комплексный логарифм

Комплексный логарифм по любому основанию

Основание логарифма

Число

Логарифм комплексного числа по комплексному основанию

Прежде, чем мы начнем речь непосредственно о логарифмах, хотелось бы поговорить о степенях чисел и их свойствах.

Действия над степенями осуществляются по следующим правилам и они Вам должны быть хорошо известны

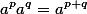
$умножение степеней$

$?{ab}^p=a^pb^p$

$(a^p)^q=a^{pq}$

$\cfrac{a^p}{a^q}=a^{p-q}$

$(\cfrac{a}{b})^p=\cfrac{a^p}{b^p}$

где a,b,p и q -произвольные числа.

В 16 веке когда возникла насущная потребность рассчитывать многозначные числа, чаще всего для астрономии и мореплавания, возник вопрос "А можно ли заменить умножение и деление многозначных чисел на более легкие операции сложения и вычитания?"

Взглянув на выше приведенные формулы , мы замечаем что то похожее в двух формулах

$a^pa^q=a^{p+q}$ и $\cfrac{a^p}{a^q}=a^{p-q}$

Осталось теперь превратить произвольное многозначное число в число вида 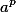$a^p$

Для некоторых чисел это известно 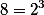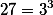$8=2^3$ $27=3^3$ и так далее, то есть любое число можно выразить в подобном виде.

число a - называется основание степени, p-степень числа

Итак у нас все готово для того что бы мы могли "заменить" умножение сложением, а деление - вычитанием.

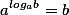
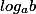
Для этого придуман логарифм, обладающим таким свойством что $a^{log_ab}=b$

$a^{log_ab}$

a - основание логарифма, которое равно численно основанию степени.

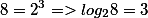
$8=2^3 => log_2{8}=3$

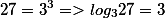
$27=3^3 =>log_3{27}=3$

Так вот, с 16-ого века, для решения задач, стали применять предварительно рассчитанные таблицы логарифов, для определенных чисел. В мои школьные годы мы использовали таблицы Брадиса.

Сейчас, при тотальной информатизации населения и товаров, наверное только наручные часы не умеют автоматически рассчитывать логарифмы.

Логарифмы обладают следующими свойствами

${log_a(uv)}=log_au+log_av$

${log_a(\cfrac{u}{v})}=log_au-log_av$

${log_a(u)}^k=k*log_au$

$log_a(u)=\cfrac{log_bu}{log_ba}$

Последняя формула примечательна тем, что с помощью можно рассчитывать логарифм любого числа (кроме нуля) и любого основания, в том числе и комплексных чисел

b- это основание логарифма и оно может быть любым. Поэтому мы можем взять за основу число e=2.718... и получим что

$log_a(u)=\cfrac{ln(u)}{ln(a)}$

Натуральные логарифы комплексных чисел мы считать уже умеем, поэтому рассчитать логарифм любого числа по любому основанию не вызовет никаких затруднений.

В основании можно кроме цифровых значений можно ввести две тестовых константы e(2.718281828459) и pi(3.1415926535898)

Если введет e - то получите значение натурального логарифма

Чему равен натуральный логарифм мнимой единицы?

Логарифм комплексного числа по комплексному основанию

Логарифм числа 0+1i
По основанию 2.718281828459
Равен = 0+1.5707963267949i

Таким образом бот помогает считать любые значения и выражения по любому основанию.

Где используются комплексные логарифмы?

Например при расчете обратных тригонометрических функций

Удачи в расчетах!