В данном материале мы рассмотрим способы вычисления и рассчитаем значения обратных тригонометрических функций в поле комплексных чисел. Результат выдается как в радианах, так и в градусах.
Арксинус комплексного числа
Если представить 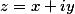
То арксинус числа, выраженный через логарифм
\(arcsin(z)=-i*ln(zi+\sqrt{1-z^2})\)
Арккосинус комплексного числа
Если представить 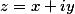
То арккосинус числа, выраженный через логарифм
\(arccos(z)=\cfrac{\pi}{2}+i*ln(zi+\sqrt{1-z^2})\)
Введите в поле число, комплексное или вещественное и программа выдаст результат
http://abak.pozitiv-r.ru
http://abak.pozitiv-r.ru
Арктангенс комплексного числа
Если представить 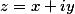
То артангенс числа, выраженный через логарифм
\(\operatorname{arctg}(z){}=\cfrac{i}{2}(ln(1-iz)-ln(1+iz))\)
Через арксинус
\(\operatorname{arctg}(z){}=arcsin\frac{z}{\sqrt{1+z^2}}\)
Через арккосинус
\(\operatorname{arctg}(z){}=arccos\cfrac{z}{\sqrt{1+z^2}}\)
Или вот так
\(\operatorname{arctg}(z){}=\cfrac{1}{2}atan(\cfrac{2x}{1-x^2-y^2})+\cfrac{i}{4}ln(\cfrac{x^2+(y+1)^2}{x^2+(y^2-1)^2})\)
Арккотангенс комплексного числа
Арккотангенс комплексного числа легко решается через связь с арктангенсом
\(\operatorname{arccotg}(z){}=\cfrac{\pi}{2}-arctg({z})\)