| Коэффицент парной корреляции(Пирсена) |
|
| Коэффицент Спирмена |
|
Корреляция является признаком, указывающим на взаимосвязь ряда численных последовательностей. Парная корреляция (Пирсена) характеризует взаимосвязь двух последовательностей xi и yi
Такой коэффициент рассчитывается по формуле
^2}{N}}\sqrt{\sum_{i=1}^Ny_i^2-\frac{(\sum_{i=1}^Ny_i)^2}{N}}})
и характеризует степень отклонения связи между xi и yi от линейной. Если абсолютное значение коэффицента близко к единице, то эта связь линейна, т.е. yi=axi+b
Причем знак коэффицента R определяет знак коэффициента а. То есть если R больше 0, то и а тоже больше нуля.
Порядковая корреляция по Спирмену
Определяется по следующей формуле.
}\sum_{k=1}^N(A_k-B_k)^2)
где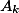 
и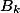 
- место (ранг) котрое занимают xk и yk при убывании xk
