Небольшой калькулятор, который позволит нам тремя измерениями заданного сегмента круга определить его радиус
Вам нужно всего три измерения и два/один инструмент: линейка +уголок(что бы отмерить прямой угол)
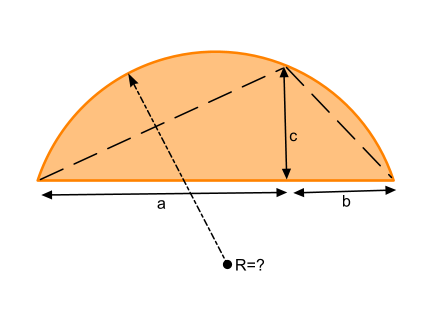
Итак, у вас есть неизвестный сегмент круга и вы измерили три значения \(a,b,c\)
Соединим точки на окружности между собой (пунктирная линия). Мы получили треугольник, с высотой \(c\) и общим основанием \(a+b\)
Этот треугольник оказывается вписанным в окружность, а мы знаем связь между площадью треугольника, его сторонами \(p, q, m\) и описанной окружностью радиусом \(R\)
\(S=\cfrac{pqm}{4R}\)
Тогда \(R=\cfrac{pqm}{4S}\)
Одна сторона нам известна \(a+b\)
две другие мы найдем по теореме Пифагора \(\sqrt{a^2+c^2}\) и \(\sqrt{b^2+c^2}\)
Осталось решить что же делать с площадью
Вспомним, что площадь треугольника равна половине произведения основания треугольника на его высоту
\(S=\cfrac{(a+b)c}{2}\)
подставим все найденные выражения и получим
\(R=\cfrac{\sqrt{a^2+c^2}\sqrt{b^2+c^2}}{2c}\)
Если бы мы выбрали \(a\) и \(b\) равными то получили бы
\(R=\cfrac{{a^2+c^2}}{2c}\)
где \(с\) - уже являлась бы высотой сегмента.