| Исходный полином |
![Вид уравнения]() |
| Факториальный многочлен имеет вид |
![Приведенное уравнение]() |
Рассмотрим одну из задач математического анализа. При вычислении конечных разностей какого либо полинома, для упрощения расчетов нам просто необходимо вычислить так называемый факториальный многочлен.
Что же он собой представляет?
Если у нас есть многочлена вида
=a_0x^{4}+a_1x^{3}+a_2x^{2}+a_{3}x+a_4)
то факториальный многочлен имеет вид
=b_0x(x-1)(x-2)(x-3)+b_1x(x-1)(x-2)+b_2x(x-1)+b_{3}x+b_4)
Алгоритм расчета коэффициентов факториального полинома очень прост.
1. Для заданного полинома берем значение k=0 и по методу Горнера узнаем частное и остаток многочлена .
2. Остаток полинома является значением коэффицента bk
3. Частное считаем за исходный полином
4. Прибавляем единицу к=к+1 и повторяем пункты 1-3
5. Прекращаем цикл если k значению высшей степени при изначальной функции.
Для факторильный многочленом имеется своё представление что бы не записывать длиннющую строку поэтому вот такой вид
Представим в виде
=b_0x^{(4)}+b_1x^{(3)}+b_2x^{(2)}+b_{3}x^{(1)}+b_4)
Пример
Задана функция
=x^{4}-8x^{3}+21x^{2}-6x+3)
Превратить её в факториальный полином
Разделим этот полином на x-0 получим
Остаток равен 3 и это значение коэффицента b4
Теперь функцию =x^3+(-8)*x^2+(21)*x^1+(-6))
разделим на x-1
|
Заданный многочлен имеет вид |
|
|
|
если разделим его |
) |
|
Получим многочлен |
=x^2+(-7)*x^1+(14)) |
|
и остаток |
 |
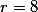Остаток равен 8 и это значение коэффицента b3
Разделим =x^2+(-7)*x^1+(14))
на x-2
|
Заданный многочлен имеет вид |
|
|
|
если разделим его |
) |
|
Получим многочлен |
=x^1+(-5)) |
|
и остаток |
 |
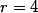Остаток равен 4 и это значение коэффицента b2
И последняя операция деления
делим =x-5)
на x-3
|
Заданный многочлен имеет вид |
=x^1+(-5)) |
|
если разделим его |
) |
|
Получим многочлен |
=(1)) |
|
и остаток |
 |
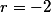Остаток равен -2 и это коэффицент b1
так как многочлен в кнце концов превратился в единицу то это и будет значением b0
Таким образом наш факториальный многочлен имеет вид
=x^{(4)}-2x^{(3)}+4x^{(2)}+8x^{(1)}+3)
Такое преобразование от обычного многочлена к факториальному виду, распрострняется и на комплексные коэффиценты, что полностью открывает область применения данного скрипта/бота.
Где могут применяться факториальные многочлены? Одно из применений это вывод формул суммы степенных рядов. Никогда бы не поверил, но это так и я попытаюсь в одной из статей рассказать Вам об этом.
Обратная конвертация из факториального многочлена в обычный расположена по адресу Из факториального полинома в обычный
=x^4+(-8)*x^3+(21)*x^2+(-6)*x^1+(3))
)
=x^3+(-8)*x^2+(21)*x^1+(-6))
