Найти число по остатку от деления

Модуль (пробел) остаток (запятая) Модуль (пробел) остаток и т.д.

Полученное число

Одна древняя китайская задача гласила:

"Найти число, которое при делении на 3 дает остаток 2, при делении на 5 дает остаток 3, а при делении на 7 дает остаток 2"

Что бы решать подобные задачи, сделаем следущее

Исходное число по исходным данным можно выразить вот так

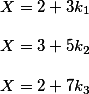
$теорема об остатках пример$

Где k - целые числа

Выпишем ряды меняя k от 0 по возрастающей

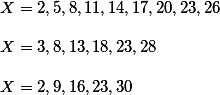
$ряд значений$

Несложно заметить что 23, встречается во всех трех рядах.

Это и есть наш ответ, следущее число (128) встретится только через 105=3*5*7 отсчетов. Так как эти числа взаимно простые, то и берем просто их произведение.

И таким образом общий ответ нашей задачи имеет вид

$X=(23)mod(105)$

Легкий алгоритм для понимания, не правда ли?

Но он не совсем неудобен, когда встречаются большие числа, и опять же, при составлении элементов ряда можно банально ошибиться.

Есть другой способ

Пусть нам дана система сравнений

$x=(c_1)mod(m_1), x=(c_2)mod(m_2)....x=(c_k)mod(m_k)$

где 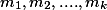$?m_1, m_2,....,m_k$ - положительные, попарно взаимно простые целые числа.

Пусть 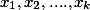$x_1, x_2,....,x_k$ - корни вспомогательных сравнений вида

$система сравнений$

Такие уравнения мы уже можем решать Сравнения 1 степени. Теория чисел.

Узнав эти корни, мы можем вычислить наше исходное число по формуле

$X=(m_2m_3...m_kx_1c_1+m1m_3...m_kx_2c_2+....+m_1m_2...m_{k-1}x_kc_k)mod (m_1m_2...m_k)$

Для нашего примера исходные данные выглядят так

$x=(2)mod(3), & x=(3)mod(5),x=(2)mod(7)$

Тогда система сравнений будет иметь вид

$(35x_1)mod(3)=1\\\\ & (21x)mod(5)=1\\\\(15x)mod(7)=1$

Решая их получим

$x_1=2, x_2=1, x_3=1$

И наше решение имеет вид

$x=35*2+21+15=106$

Или то же самое что и

$x=(233)mod(105)=(233-105-105)mod(105)=23mod(105)$

Как видите, ответ совпадает.

Наш бот решает подобные задачи используя библиотеку PHP GMP. Поэтому к точности расчетов и ограничений на длину значений, это к ним :)

Хотя есть и свои материалы в частности: Расчет значения функции Эйлера, Остаток числа в степени по модулю и Диофантовое уравнение с тремя неизвестными

Важно: Логично и это надо учитывать при ввводе чисел, в паре чисел (модуль- остаток), модуль (всегда!) больше чем остаток.

Второе важное замечание. Модуль всегда(!) положительное число, остаток, может быть отрицательным, но лучше все таки привести его к положительному числу.

Как это сделать? Все ссылки на сопутствующие материалы уже приведены.

Пример

Узнать какое загадано число, если остаток при делении его на 37 равно 11, при делении на 9 равно 4, при делении на 7 равно 1, а при делении на 100 остаток равен 25.

Заметим, что модули, то есть числа (37, 9, 7, 100) на которые мы делим неизвестное число, попарно взаимно простые. То есть у нас нет ни одной пары из этих чисел, так что бы они имели общий делитель.

Раз так, то мы можем решать подобную задачу тем, методом который описан выше.Вводим в поле ввода

37 11, 9 4, 7 1, 100 25

За мгновение получим ответ

Полученное число

$Полученное число$

Удачных расчетов!

Поиск по сайту