Разложить многочлен по степеням

Коэффициенты многочлена разделенные пробелами

Коэффицент C в биноме вида x-C

Заданный многочлен имеет вид

если разложим по степеням вида

Получим многочлен

В данном материале мы рассмотрим как можно разложить произвольный многочлен от одной переменной по степеням

Практические задачи, которые попадаются в учебниках и которые можно решить с помощью бота, выглядят вот так:

Разложить на простейшие дроби рациональную дробь

$\cfrac{x^3+2x-3}{(x+3)^4}$

или

Разложить многочлен по степеням x многочлен $f(x-3)$ где $f(x)=x^5-5x^4-4x^3+2$

И тот, и другой пример можно решить используя метод Горнера , только необходимо этот метод применить столько раз, сколько имеет максимальное значение степени при неизвестном.

Сначала рассмотрим последний пример

Разложим по методу Горнера заданный многочлен на вот такое значение $(x-3)$

Почему стоит минус, а не плюс как в исходной задаче, спросите Вы. Не торопитесь, всему своё время.

$\cfrac{x^5-5x^4-4x^3+2}{x-3}=x^4-2x^3-10x^2-30x^1-90-\cfrac{268}{x-3}$

Запомним остаток -268

и разделим уже полученный многочлен 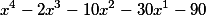$x^4-2x^3-10x^2-30x^1-90$ опять на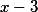 $(x-3)$

получим 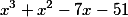$x^3+x^2-7x-51$ и остаток -243

Еще раз проделаем операцию деления

получим 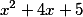$x^2+4x+5$ и остаток -36

Еще раз проделаем операцию деления

получим 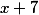$x+7$ и остаток 26

Еще раз проделаем операцию деления

получим $x$ и остаток 10

Еще раз проделаем операцию деления

получим ----- и остаток 1

Теперь составим из наших остатков вот такой многочлен

$f(x)=(x-3)^5+10(x-3)^4+26(x-3)^3-36(x-3)^2-243(x-3)-268$

Вот это нам будет считать бот автоматически, а две последующие строки мы делаем вручную

Теперь заменим 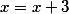$x=x+3$ и получим

$f(x+3)=x^5+10x^4+26x^3-36x^2-243x-268$

Вот и всё. Поняли почему мы раскладывали множитель на $(x-3)$ а не $(x+3)$ ?

Бот выдает результирующий многочлен с несколько избыточным количеством скобок. Не думаю что это у Вас вызовет какое либо раздражение.

Разложение по степеням многочлена может осуществляется так же и в комплексной плоскости, то есть все коэффициенты могут быть комплексными числами.

Давайте рассмотрим пример первый

Разложить на простейшие дроби рациональную дробь

$\cfrac{x^3+2x-3}{(x+3)^4}$

Логично предположить что нам числитель 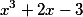$x^3+2x-3$ необходимо разложить по степеням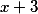 $(x+3)$

получим результат $https://img.abakbot.ru/cgi-bin/mathtex.cgi?f(x)=(x-(-3))^3+(-9)*(x-(-3))^2+(29)*(x-(-3))^1+(-36)$

и наш ответ будет такой

$f(x)=\cfrac{1}{x+3}-\cfrac{9}{(x+3)^2}+\cfrac{29}{(x+3)^3}-\cfrac{36}{(x+3)^4}$

Если Вы попали на эту страницу, ища ответ на вопрос наподобие вот этого "как разложить в произведение множителей число 1800" то Вам несомненно стоит прочитать материал Простые множители. Теория чисел

Удачных расчетов!

Поиск по сайту