| Уравнение кривой второго порядка |
![Уравнение кривой]() |
| Уравнение прямой к угловым коэффициентом |
![Уравнение прямой]() |
| Координаты пересечения кривой и прямой |
![Первая координата]() |
![Вторая координата]() |
Продолжим наш анализ кривых второго порядка и сейчас мы готовы представить сервис который позволяет рассчитывать точки пересечения произвольной прямой и произвольно заданной кривой второго порядка. Таким образом бот позволяет рассчитывать точки пересечения:
- прямой и параболы
- прямой и эллипса
- прямой и окружности
- прямой и гиперболы
- прямой и параболы
Для тех посетителей кому интересно, сообщаем общую формулу расчета точек пересечения кривой второго порядка и прямой
Если прямая представлена в виде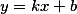 
, а кривая в виде 
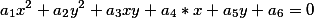то решая квадратное уравнение вида
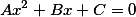
где
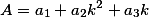
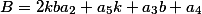
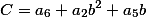
получаем две точки абсцисс 
, которые являются корнями квадратного уравнения.
поставив эти значения в уравнение прямой 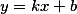, мы определяем две точки ординат и таким образом у нас есть пара точек пересечения прямой и кривой.
Синтаксис для XMPP клиентов
kp2_line параметры прямой;kp2=коэффициенты кривой через пробел
параметры прямой - могут быть различны. лучше по этому вопросы прочитать статью Расчет параметров прямой линии по заданным параметрам
коэффициенты кривой - формат такой же как в статье Расчет кривых второго порядка на плоскости
Примеры использования
Найти точки пересечения прямой проходящей через точки (0, 2) и (-3,-8) и параболы заданная уравнением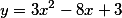 
Прямая задана двумя точками. Обратившись к вышеупомянутной статье по расчету прямой линии мы видим, что параметры линии надо записать так
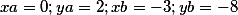
а коэффициенты кривой второго порядка имеют вид 3 0 0 -8 -1 3
Теперь мы записываем все данные
kp2_line xa=0;ya=2;xb=-3;yb=-8;kp2=3 00 -8 -1 3
и получаем результат
Точки пересечения кривой второго порядка вида
( 3 ) x^2 + ( -8 ) x + ( -1 ) y + ( 3 ) = 0
и прямой вида
y = 3.3333333333333*x + (2)
Первая координата x = 3.6874 y = 14.291333333333
Вторая координата x = 0.0904 y = 2.3013333333333
Определить координаты пересечения прямой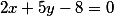 
и окружности ^2+(y+1)^2=25)
Для решения этой задачи нам придется раскрыть скобки для уравнения окружности
результат будет вот такой ^2+(y+1)^2-25=x^2-6x+9+y^2+2y+1-25=x^2+y^2-6x+2y-15)
Таким образом коэффициенты кривой будут вот такие
1 1 0 -6 2 -15
а коэффиценты прямой запишем вот так
A=2;B=5;C=-8
и общий вид запроса будет вот такой
kp2_line A=2;B=5;C=-8;kp2=1 1 0 -6 2 -15
Ответ бота
Точки пересечения кривой второго порядка вида
( 1 ) x^2 + ( 1 ) y^2 + ( -6 ) x + ( 2 ) y + ( -15 ) = 0
и прямой вида
y = -0.4*x + (1.6)
Первая координата x = 7.9655 y = -1.5862
Вторая координата x = -1.0000 y = 2
Истинность расчетов легко проверяется подстановкой в уравнение прямой или окружности
Прямая пересекает ось абсцисс под углом 50 градусов и проходит через точку (2,-1). Определить точки пересечения данной прямой и эллипса который проходить через три точки (3,-2) (3,1) (-6,-1)
Несмотря на то, что нет ниодного явного уравнения, бот сможет Вам дать правильный ответ
Для прямой линии известны два параметра это координаты точки и угловой коэффициент.
Угловой коэффициент связан с углом к оси абсцисс следующим выражением
)
где F - это угол в радианах, а k - это угловой коэффициент
тогда зная угол в 50 градусов, угловой коэффициент равен 1.19175359259421
k=1.19175359259421;xa=2;ya=-1
А для кривой второго порядка зная, что эллипс может быть выражен в виде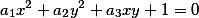 
запишем данные таким образом 3:-2 3:1 -6:-1 0 0 1
kp2_line k=1.19175359259421;xa=2;ya=-1;kp2=3:-2 3:1 -6:-1 0 0 1
Получаем ответ
Точки пересечения кривой второго порядка вида
( 0.022222222 ) x^2 + ( -0.600000000 ) y^2 + ( -0.200000000 ) xy + ( 1 ) = 0
и прямой вида
y = 1.1917535925942*x + (-3.3835071851884)
Первая координата x = 1.4997 y = -1.5962343223749
Вторая координата x = 3.6632 y = 0.98212457520267
Удачных расчетов!!
