Поиск углового коэффициента прямой, отрезка
Угловой коэффицент прямой - это тангенс угла, под которым заданная прямая пересекает ось абсцисс. Несложно из этого понять что линия которая проходит паралельно оси Х имеет коэффицент равный нулю, а которая перпендирулярна оси абсцисс имеет коэффициент стремящийся к бесконечному числу.
Как же можно рассчитать угловой коэффицент?
По двум координатам прямой
| Уголовой коэффициент заданной прямой |
|
| Следовательно прямая пересекает ось абсцисс под углом |
|
По отрезкам на осях, которые пересекает заданная прямая
Это очень элементарно. С учетом первого предложения статьи, где давалось определение углового коэффициента, зная значения отрезков оси, угловой коэффициент определяется как отношение противолежащего отрезка оси ординат, к прилежащему отрезку оси абсцисс.
По заданным параметрам нормального уравнения прямой
Нормальное уравнение прямой имеет вид
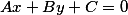
Представив x=0 мы узнаем что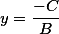 
То есть прямая пересекает ось ординат в этой точке
А если подставив y=0 то узнаем что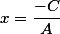 
. То есть прямая пересекает ось абсцисс в этой точке
А зная что угловой коэффицент это отношение y к x получим что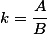 
Этот материал основан на более универсальном калькуляторе Расчет параметров прямой линии по заданным параметрам
