Кубическое уравнение. Альтернативный взгляд.

Во всех материалах которые встречаются в ТОП-10, решение кубического уравнения сводится к формулам Кардано. Эти формулы правильные и наверное по своему красивы, но нет них в той элегантности как хотелось бы.

Это касается и тригонометрических формул Виета, хотя конечно выводятся / доказываются они просто, но...

Предлагается, немного другой взгляд на решение кубического уравнения вида 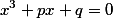$x^3+px+q=0$

$\phi=atan(\frac{1}{q}\sqrt{Discriminant})$

Где дискриминант - является результатом деления стандартного (классического дискриминанта) на число 27.

$Discriminant=-q^2-4\frac{p^3}{27}$

Формула настолько элегантна и проста, что хочется взять и распространить её на уравнения 4, 5 и более степеней. Но увы, с наскока получить примлемое решение не удалось, хотя наверяка решение где то рядом.

Заметим что это формула прекрасно работает и в поле комплексных чисел.

Давайте вообще избавимся от дискриминанта.

Тогда

$\phi=atan(\sqrt{\frac{Discriminant}{q^2}})$

$\phi=atan(\sqrt{\frac{q^2+\frac{4p^3}{27}}{-q^2}})=atan(\sqrt{{-1-\frac{4p^3}{27q^2}}})$

$\phi=atan(\sqrt{\frac{Discriminant}{q^2}})$

где i - это мнимая единица.

Можно еще преобразовать формулу и получим вот такой вид

$x_i=2i\sqrt{\frac{p}{3}}cos(\frac{\phi+2i\pi}{3})}, i=0,1,2$

Если мы попробуем преобразовать арктангенс через арккосинус, то получим всем известную формулу Виета.

$\phi=atan(i\sqrt{\frac{(\frac{q}{2})^2}{(\frac{-p}{3})^3})$

$x_i=2i\sqrt{\frac{p}{3}}cos(\frac{\phi+2i\pi}{3})}, i=0,1,2$

В принципе откуда вышли, туда и пришли, но речь в принципе не только об этом.

Все таки не хватает элегантности...

Я пытаюсь поставить себя на место преподаватели, потом ученика и никак не могу объяснить с одной стороны, а с другой стороны понять, зачем при решении кубического уравнения мы изучаем формулы Кардано.

На мой взгляд, это все равно что изучать латынь в настоящее время, потому что раньше было так принято.

Решение неполного кубического уравнения сводится через коэффициенты полинома Чебышева в еще более простую формулу.

Если обозначить $T_n(x)=cos(nacos(x))$ n-ый полином Чебышева, то решение кубического уравнения сводится с формуле

$x_i=2i\sqrt{\frac{p}{3}}cos(\frac{\phi+2i\pi}{3})}, i=0,1,2$

В отличие от формул/расчетов 13 века, эта формула компактнее, красивее, удобнее.

Жаль только что полиномы 4 и выше степеней не решаются так же просто как и кубический многочлен.

Поиск по сайту