| Заданные вектора и результирующий вектор |
![Уравнение]() |
Умножение двух векторов в пространстве
Достаточно простая задача которая встречается в школьных учебниках: Найти векторное произведение двух векторов
Например: ) и
и )
Одним из способов решения является матричный метод
i - ( 7 )j + ( -10 )k)
Таким образом наш результирующий вектор имеет значения
)
Все вычисления проивзодятся в правой системе координат. Если же вам надо умнодить вектора в левой системе координат, то каждый результирующее значение надо взять с обратным знаком.
В левой системе координат наш ответ будет )
Расширение исходной темы
Рассмотрим более общую задачу как вычислить "результирующий вектор" когда есть матрица без одной верхней строки. Вернее, каждый элемент верхней строки является неизвестной величиной- переменной.
Когда у нас есть вот такая матрица
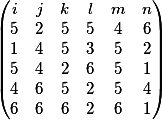
И необходимо разложить её в "вектор"
Практического применения я пока еще не нашел, но сама идея интересная и главное, при возникновении такой задачи для вас упрощаются все вычисления.
Update 04.01.2019. Практическое применение найдено, с помощью такого "расширенного вектора" достаточно легко решаются неоднородные линейные системы уравнений. Кому интересно просьба ознакомится: Общее решение неоднородной системы уравнений
Итоговым решением заданной матрицы будет выражение.
i + ( 1127 )j + ( 1108 )k +\\\\+ ( 1046 )l + ( -2426 )m + ( -490 )n)
Естественно все это работает и в поле комплексных чисел.
То есть если у нас есть матрица
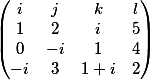
То результирующий вектор имеет вид
i + ( -2-1i )j + ( -7-10i )k +\\\\+ ( 2+2i )l)
Ограничение опять же одно - матрица не более чем 10 на 10.
Надеюсь это поможет кому то в работе.