Гиперболические функции комплексного числа
| Гиперболический синус числа |
![Гиперболический синус]() |
| Гиперболический косинус числа |
![Гиперболический косинус]() |
| Гиперболический тангенс числа |
![Гиперболический тангенс]() |
| Гиперболический котангенс числа |
![Гиперболический котангенс]() |
| Если исходное число было в градусах, то |
| Гиперболический синус числа (если заданное число было в градусах) |
![Гиперболический синус в градусах]() |
| Гиперболический косинус числа (если заданное число было в градусах) |
![Гиперболический косинус в градусах]() |
| Гиперболический тангенс числа (если заданное число было в градусах) |
![Гиперболический тангенс в градусах]() |
| Гиперболический котангенс числа (если заданное число было в градусах) |
![Гиперболический котангенс в градусах]() |
В статье рассматривается способы расчета и выдача значений гиперболических фунций от комплесного числа
Гиперболический синус комплексного числа
Если представить комплексное число как 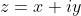
То гиперболический синус числа, выраженный через экспоненту комплексного числа
=\frac{e^z-e^{-z}}{2})
Гиперболический косинус комплексного числа
Если представить 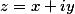
То гиперболический косинус числа, выраженный через экспоненту
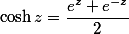
Введите в поле число, комплексное или вещественное и программа выдаст результат
http://abak.pozitiv-r.ru
http://abak.pozitiv-r.ru
Гиперболический тангенс комплексного числа
Если представить 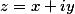
То гиперболический тангенс числа, выраженный через гиперболический синус и гиперболический косинус
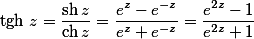
Гиперболический котангенс КОМПЛЕКСНОГО ЧИСЛА
Гиперболический котангенс комплексного числа решается как обратная величина гиперболического тангенса.
})