Рассмотрим, один из способов вывода формулы по которой определяется сумма геометрической прогрессии. Есть несколько способов доказательств, в том числе и через пределы. Но мы пойдем простым и логичным путем, не плодя новых сущностей, и не забивая голову, в данном случае тем, что для решения этой задачи нам не пригодится.
Напомним, что бесконечная сумма геометрической прогресии существет и ограничена в том случае, если каждый из последующих элементов стремится к нулю. Или как написано в разных учебниках абсолютное значение знаменателя прогрессии меньше единицы.
Напомним, что же считается геометрической прогрессией?
Последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (q - знаменатель прогрессии) и называется геометрической прогрессией.
Любой член геометрической прогрессии может быть вычислен по формуле:
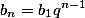
а сумма прогрессии( считаем что она бесконечна, т.е. знаменатель не меньше нуля и не больше единицы) равна
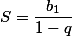
Попробуем решить следующую задачу найти сумму бесконечной геометрической прогрессии, заданную рядом
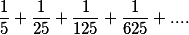
Смотрим на неё и размышляем. Что же мы можем с ней сделать, не зная ни одной формулы? Ну как минимум можем вынести  за скобки.
за скобки.
Попробуем +frac{1}{25)+frac{1}{125)+frac{1}{625)+....)
)
Аха! В скобках получился такой же ряд что и в начале только с единицей в начале.
Обозначим сумму ряда как S
и тогда можем записать что
=S)
Это уравнение с одной переменной и легко решается
Ответ  . Это и есть наш ответ.
. Это и есть наш ответ.
Заметили? Мы не пользовались ни пределами, не запоминали ни одну формулу. Мы просто здраво рассуждали и пришли к правильному решению.
Давайте обобщим и выведем общую формулу геометрической прогрессии вышеуказанным способом.
У нас есть ряд 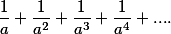
Обозначим эту сумму как S и вынесем  за скобки
за скобки
получим )
или =S)
Отсюда 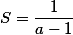
Возросла самооценка от того, что сами можете доказывать и выводить формулы?
То то же :)