| Рассчитываем элементы непрерывной дроби для числа |
![Введенное выражение]() |
| Полученный результат.Числитель |
| |
| Знаменатель |
| |
| Непрерывная дробь |
| |
Цепная или непрерывная дробь - это дробь которую можно отобразить в виде
\(m/n=a0+\cfrac{1}{a1+\cfrac{1}{a2+\cfrac{1}{a3+ ...}}}\)
Цепочку из элементов a0,a1,a2,a3 и т.д. чаще всего представляют в виде строки [a0,a1,a2,a3,a4.....an]
Как пример покажем как можно представить дробь 52/111 в виде цепной дроби
\(52/111=0+\cfrac{1}{2+\cfrac{1}{7+\cfrac{1}{2+\cfrac{1}{3}}}}\)
Применение цепных дробей достаточно велико.
Мы можем с помощью них находить приближенные значения иррациональных чисел.
Непрерывная дробь иррационального квадратного корня всегда имеет вид
Таким образом мы можем утверждать что цепная дробь периодическая.
Мы можем сокращать дроби и в идеальном случае создавать калькулятор дробных чисел, не обращая внимания на то, какие числа в выражении будут фигурировать.
Для любознательных и юных математиков, покажется очень интересным материал позволяющим по элементам непрерывной, цепной дроби (в том числе и комплексной) получать результирующую дробь(Результат по комплексной цепной дроби). Анализ таких цепей при разных начальных условиях, дает широкую возможность оценить свои силы и возможности понимания этой части такой науки как арифметика.
Для тех пользователей кто попал сюда в поисках вычисления дробных выражений то Вам вот на этот ресурс Калькулятор правильных и неправильных дробей
Попробуем решить
12*(12/17+11/13) -2.4
Пишем это выражение как есть и получаем результат
| Рассчитываем элементы непрерывной дроби для числа |
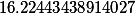 |
| Полученный результат.Числитель |
|
17928
|
| Знаменатель |
|
1105
|
| Непрерывная дробь |
|
16 4 2 5 7 2 1
|
Пример3
Попробуем сократить заданную дробь 62345346 / 786786. Хотелось бы заметить что это так же задачей по нахождению
наибольшего общего делителя.
Пишем 62345346/786786
ответ
| Рассчитываем элементы непрерывной дроби для числа |
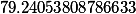 |
| Полученный результат.Числитель |
|
1484413
|
| Знаменатель |
|
18733
|
| Непрерывная дробь |
|
79 4 6 2 1 4 2 1 3 4
|