| Расстояние от центра шара (вправо и влево) |
|
| Длина "хорды" n-ого рассечения |
|
Рассмотрим задачу рассечения шара параллельными плоскостями, с произвольным радиусом \(R\), на \(n\) частей, равных между собой по объему.
Подобную задачу на рассечение мы уже решали, но там речь шла о плоском круге. Рассечение круга прямыми на равные площади
Теперь, так как речь идет об объемной фигуре, будем высчитывать какой высоты необходимо отрезать очередной кусок от нашего "колобка", так что бы объемы этих "отрезов" были одинаковы.
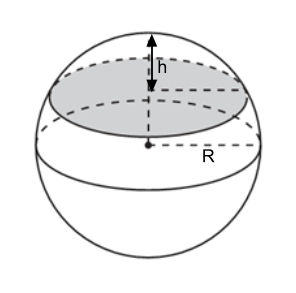
При любом количестве рассечений шара, мы всегда получаем "горбушку" от шара - шаровой сегмент.
Объем его высчитывается по формуле
\(V=h^2\pi(R-\cfrac{h}{3})\)
С другой стороны объем шара равен \(V=\cfrac{4}{3}R^3\pi\)
n-ая часть этого шара равна \(V=\cfrac{4}{3n}R^3\pi\)
Приравняв, получим \(h^2\pi(R-\cfrac{h}{3})=\cfrac{4}{3n}R^3\pi\)
Преобразовав, получим следующее
\(\cfrac{4}{n}=3(\cfrac{h}{R})^2-(\cfrac{h}{R})^3\)
заменим \(\cfrac{h}{R}=x\)
Получили красивое кубическое уравнение
\(\cfrac{4}{n}=3x^2-x^3\)
зная как решается уравнение вида \(x(x+a)^2+c=0\)
\(x_i=\cfrac{-4a}{3}cos(\cfrac{acos(-1-\cfrac{\cfrac{c}{2}}{\cfrac{-a^3}{3^3}})}{6}+\cfrac{k2\pi}{6})^2\)
мы после преобразований получим
\(x_i=-4*cos^2(\cfrac{acos(-1+\cfrac{2}{n})+2k\pi}{6})+3\)
Или еще упростив
\(x_i=-2*cos(\cfrac{acos(-1+\cfrac{2i}{n})}{3}+\cfrac{4\pi}{3})+1\)
где \(i\) - номер отрезаемой части
Корни и будут являться нашим решением, не забывая сделать обратное преобразование \(\cfrac{h}{R}=x\)
Проверим если частей пять а радиус шара равен единичному номиналу (1 м, или 1 км, или 1 парсек не важно)
Результат просто берете в тех же измерениях
| Расстояние от центра шара (вправо и влево) |
|
\\0.5742815\\0.86586220.5742815
0.8658622
|
| Длина "хорды" n-ого рассечения |
|
\\1.8097113\\1.98192541.8097113
1.9819254
|
Удачных расчетов!!