| Расстояние от центра круга (сначала все точки вправо, потом влево) |
|
| Длина хорды n-ого рассечения |
|
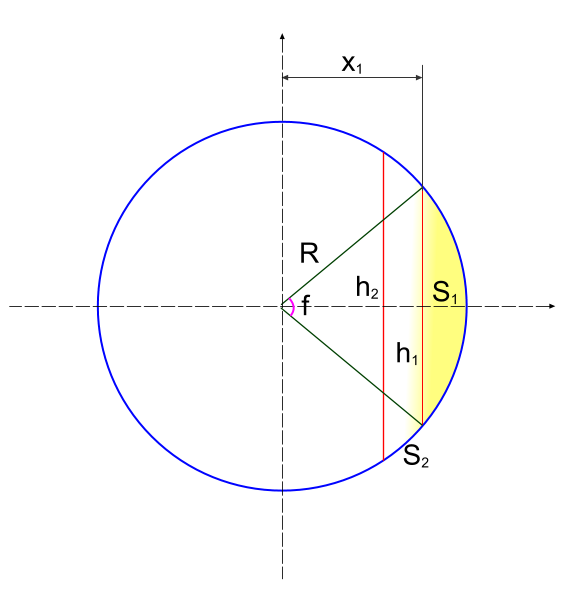
Рассмотрим простую задачу - как рассечь параллельными прямыми круг на N - частей с одинаковой площадью. Используем только формулу сегмента круга и свои умозаключения.
Любое деление круга на равные части подразумевает что у нас всегда будет круговой сегмент S. Площадь его известна
\(S_1=\cfrac{R^2}{2}(f-sin(f))\)
Раз мы делим круг на n частей то логично что площадь каждого "куска" должна составлять \(S_1=\cfrac{\pi{R^2}}{n}\)
приравняв два вышеуказанных уравнения, мы получим связь угла с числом разбиений
\(\cfrac{2\pi}{n}=f-sin(f)\)
Второй сегмент будет в два раза больше и поэтому \(\cfrac{2*2\pi}{n}=f-sin(f)\)
Видим, что от радиуса они совсем не зависят.
Тогда отсчитывая вправо мы можем узнать на каком расстоянии от центра круга мы должны провести очередную прямую.
\(x_n=Rcos(\cfrac{f}{2})\)
Не забудьте потом отмерить такое же расстояние от центра и влево тоже.
Хорда, то есть часть прямой которая проходит через круг и отсекает от него очередной сегмент имеет длину
\(h_n=2Rsin(\cfrac{f}{2})\)
Вот в принципе весь расчет.
При четном разбиении одна из линий всегда будет проходить через центр окружности.