Корни характеристического уравнения

3 -1 1 -1 5 -1 1 -1 3

Исходная матрица

Характеристическая матрица

Характеристический полином

Его корни

По заданным элементам матрицы  вычисляется его характеристическое уравнение, и находятся его корни. Ограничение сверху  - матрица не больше 4 на 4, так как только для уравнения 4 степени, создан калькулятор. 

 

Чем хорош данный калькулятор? Тем что работает в поле комплексных чисел, то есть исходные данные могут быть и вещественными и мнимыми.

Кроме этого, кроме значений можно писать любое математическое уравнение, которое корректно вычислется универсальным калькулятором комплексных чисел, что очень упрощает работу

Для чего нужны характеристические уравнения? 

- Приведение поверхности или кривой 2 порядка  в канонический вид

- Исследование дифференциальных уравнений на устойчивость

- Определение Жордановой формы матрицы

- Анализ матрицы квадратичной формы

и многое другое.

Рассмотрим несколько примеров:

Найти общее характеристическое уравнение и его корни, если дана матрица

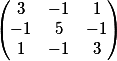
Введя данные слева направо, сверху снизу мы получим следующий результат

Исходная матрица

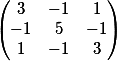Характеристическая матрица

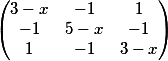Характеристический полином

Его корни

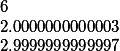Корни полинома 2, 3 и 6. Идет небольшая погрешность, в 15 знаке, но я считаю что это некритично.

Еще один пример

И ответ

Исходная матрица

Характеристическая матрица

Характеристический полином

Его корни

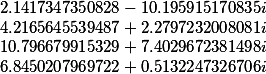Удачных расчетов!

 

• << Корни уравнения типа x^3n+Ax^2n+B=0
• Коэффициенты полинома Чебышева. Свойства >>