Расчет квадратного, кубического и 4 степени уравнения онлайн

Аргументы уравнения 1, 2,3 и 4 степени

Точность вычисления (знаков после запятой)

Вы ввели следующее выражение

Результат решения заданного уравнения

Линейные уравнения - те самые "цветочки" математического анализа, которые любой школьник и студент обязан щелкать, как земляные орешки. Уравнения первого порядка, квадратные, кубические, уравнения четвертой степени - все они относятся к азам математики, не знать которые - преступление для взрослого человека. Но когда таких расчетов сотни и приходится выполнять их очень быстро, возникает желание как-то автоматизировать сей процесс. Например, вбивать в онлайновый калькулятор только коэффициенты и радоваться вычисленным машиной корням.

Чтобы не заблудиться в уравнениях и не удивляться, откуда взялись на экране ложные результаты, стоит вспомнить теоретическую подоплеку каждого из обсуждаемых уравнений.

Уравнение первой степени с единственной переменной - это равенство вида $ax + b = 0$ , где х - искомое число, а $a$ и $b$ { -определенные действительные (!) числа. Если a = b = 0, то в качестве решения уравнения выступает любое число, если оба этих числа приравнены к нулю, у уравнения решений нет, а если a и b существуют, то уравнение начинает называться линейным, и $x=-\frac{b}{a}$

Святая простота линейного уравнения первой степени плавно перетекает в такой же простой дискриминант для квадратного уравнения: 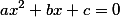ax^2 + bx + c = 0 , вычисляемый по формуле 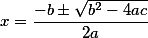$x={-b\pm\sqrt{b^2-4ac} \over 2a}}$ . С первого взгляда формула выглядит страшновато - еще один повод обратить внимание на АБАК, который требует указания одних только действительных коэффициентов a, b, c и сам выдает множество решений.

Корни кубического уравнения 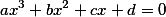ax^3 + bx^2 + cx + d = 0 уже имеют все шансы испугать непосвященного в математику человека, так как ему придется заменой 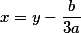$x=y-\dfrac {b } {3a}$ привести исходное уравнение к каноническому виду 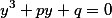y^3 + py + q = 0 , где числом 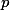выступает выражение 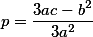$p=\dfrac {3ac-b^{2}} {3a^{2}}$ , а 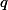заменит громоздкий трехчлен 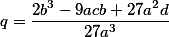$q=\dfrac {2b ^{3}-9acb +27a^{2}d} {27a^{3}}$ . Корни нового уравнения с заменой 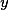на вычисляются вот так

$Q=\left( \dfrac {p} {3}\right) ^{3}+\left( \dfrac {q} {2}\right) ^{2}$ .

$\alpha=\left( -\dfrac {q} {2}+\sqrt {Q}\right) ^{\dfrac {1} {3}}$

$\beta=\left( -\dfrac {q} {2}-\sqrt {Q}\right) ^{\dfrac {1} {3}}$

$y_{1}=\alpha +\beta$

$y_{2,3}=-\dfrac {\alpha+\beta } {2}\pm i\dfrac {\alpha-\beta } {2}\sqrt {3}$

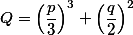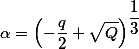
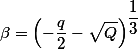
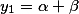
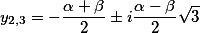
АБАК благополучно прячет от пользователя все эти тонкости, выдавая красивое решение с нужной точностью

Решение уравнения 4 степени будет еще сложнее и поэтому в рамках этого проекты мы его не рассматриваем подробно.

Кстати можно решить и обратную задачу, по известным корням многочлена узнать общий вид этого многочлена. Для этого необходимо воспользоваться материалом Создание полинома (многочлена) одной переменной онлайн

Итак, решить любое из описанных уравнений с помощью карандаша, бумаги и знаний,

Выдает все корни, в том числе и комплексные значения.

Поиск по сайту