Основные комбинаторные соотношения в теории вероятностей

В теории вероятностей, при подсчете числа исходов испытаний(попыток) применяют следующие соотношения

Число перестановок по m элементов из n различных элементов, в которых каждый элемент используется только один раз.

$P(n,n)=A_n^m$

$A_n^m=\frac{n!}{(n-m)!$

В частности, число перестановок из n различных элементов равно

$P(n,n)=n!$

Число перестановок по m элементов по n различных элементов, в которых каждый элемент может использоватся любое допустимое (от 0 до m) число раз

$U(n,n)=n^m$

Таким способом мы например высчитывали какой же запас автомобильных номеров может существовать при той или иной нумерации.

Число перестановок из n элементов, среди которых n₁ первого вида, n₂ второго вида,...n_m m-ого вида, или число способов рзмещения n различных элементов по m различным ячейкам при условии, что в i-ой ячейке помещается n_i(i=1,...,m) элементов

$P(n;m_1,...m_k)=C_n^{m_1,....,m_k}$

где

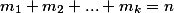
$m_1+m_2+...+m_k=n$

Число перестановок из n различных элементов, в которых имеется ровно k несмещенных элементов(относительно исходного их расположения)

$D(n,k)=C_n^k(n-k)![\sum_{i=0}^{n-k}\frac{(-1)^i}{i!}]=C_n^kD_{n-k}$

Значение 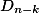$D_{n-k}$ - есть субфакториал и рассчитывается по реккуретной формуле

$D_n=nD_{n-1}+(-1)^n$

при $D_0=1$

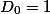
Число сочетаний по m элементов из n различных элементов, в которых каждый элемент используется только один раз

$C(n,m)=C_n^m$

Число сочетаний по m элементов из n различных элементов, в которых каждый элемент может повторятся любое допустимое (от 0 до m) число раз

$f(n,m)=C_{n+m-1}^m=C_{n+m-1}^{n-1}$

Число размещений m одинаковых элементов по n различным ячейкам при условии, что n-k из них остаются пустыми

$C_n^kC_{m-1}^{k-1}=C_n^{n-k}C_{m-1}^{k-1}\\\\(m\ge{k},1\le{k}\le{n}$

а число всевозможных размещений

$\sum_{k=1}^nC_n^{n-k}C_{m-1}^{k-1}=C_{n+m-1}^{n-1}=f(n,m)$

Число размещений m различных элементов по n различным ячейкам при условии, что n-k из них остаются свободными

$A_n^kS(m,k), (m\ge{k},1\le{k}\le{n})$

а число всевозможных размещений

$\sum_{k=1}^nA_n^kS(m,k)=N^m=U(n,m)$

Число размещений m различных элементов по n одинаковым ячейкам при условии, что n-k из них остаются свободными

$S(m,k), (m\ge{k},1\le{k}\le{n})$

а число всевозможных размещений

$V(n,m)=\sum_{k=1}^nS(m,k)$

Число размещений m одинаковых элементов по n одинаковым ячейкам при условии, что n-k из них остаются свободными

$p_m(k),(m\ge{k},1\le{k}\le{n})$

а число всевозможных размещений

$F(n,m)=\sum_{k=1}^np_m(k)$

Для правильного пользования приведенными комбинаторными соотношениями надо уяснить различие размещений при разных и одинаковых ячейках и элементах. Возможные комбинации условий и выражения для числа размещений при каждой комбинации приведены в таблице.

Ячейки, n	Элементы,m
Ячейки, n	различные	одинаковые
различные	U(n,m)	f(n,m)
одинаковые	V(n,m)	F(n,m)

Поиск по сайту